【题目】如图1,已知菱形![]() 的边长为12,
的边长为12,![]() , 点
, 点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() .
.
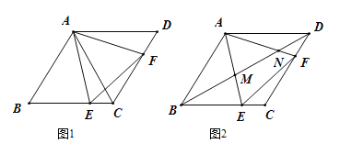
(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)如图2,连接![]() 分别与边
分别与边![]() 、
、![]() 交于
交于![]() 、
、![]() ,当
,当![]() 时,求证:
时,求证:![]()
![]() .
.
参考答案:
【答案】(1)见解析;(2)不变,![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)证明△ACE≌△ADF,证出AE=AF,结合![]() ,便证出△AEF是等边三角形;
,便证出△AEF是等边三角形;
(2)根据△ACE≌△ADF,则四边形![]() 的面积等于△ABC或者△ACD的面积.
的面积等于△ABC或者△ACD的面积.
(3)将△ADN绕点A顺时针旋转120°得到△ABP,连接PM.结合旋转的性质证明△MAN≌△MAP,根据四边形ABCD是菱形,∠ABC=60°,推出∠BPM=90°,即可证明结论.
(1)在菱形ABCD中,∵∠B=60°,
∴△ABC是等边三角形,∠D=∠B=60°,
∴AB=BC=AC,∠ACB=60°,
∴AC=AD,
∵![]() ,
,
∴∠CAE=∠DAF,
又∵∠D=∠ACE=60°,
∴△ACE≌△ADF,
∴AE=AF,
∴△AEF是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积不变.
的面积不变.
理由:
∵△ACE≌△ADF,
∴![]() ,即
,即![]()
![]() ;
;
(3)将△ADN绕点A顺时针旋转120°得到△ABP,连接PM.
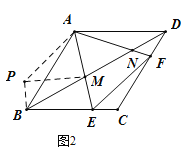
∵∠DAF=15°,∠EAF=60°,∠BAD=120°,
∴∠BAE=45°,∠BAP=∠DAF=15°,
∴∠MAN=∠MAP=60°,
∵AM=AM,AN=AP,
∴△MAN≌△MAP(SAS),
∴MN=PM,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ADN=![]() ∠ADC=30°,
∠ADC=30°,
∴∠AND=180°-15°-30°=135°,∠ANM=45°,
∴∠APB=∠AND=135°,∠APM=∠ANM=45°,
∴∠BPM=90°,
∴BP2+PM2=BM2,
∵BP=DN,PM=MN,
∴DN2+MN2=BM2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的
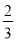 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.2万元,乙队每天的施工费用为5.8万元.工程预算的施工费用为501万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为1cm/s.

(1)当E与F不重合时,四边形DEBF是平行四边形吗?说明理由;
(2)若BD=8cm,AC=12cm,当运动时间t为何值时,以D、E、B、F为顶点的四边形是矩形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
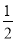 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).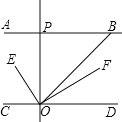
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移得到△A1B1C1的面积.求:
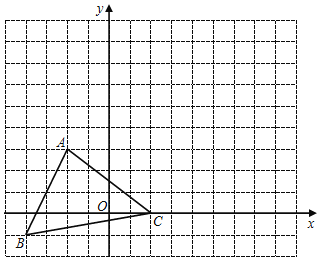
(1)画出△A1B1C1和写出点B1的坐标;
(2)写出平移的过程;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )

A.∠ABC=2∠CB.∠ABC=
 ∠CC.
∠CC. ∠ABC=∠CD.∠ABC=3∠C
∠ABC=∠CD.∠ABC=3∠C -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
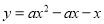 (
( 为非零常数).
为非零常数).(
 )若对称轴是直线
)若对称轴是直线 .
.①求二次函数的解析式.
②二次函数
 (
( 为实数)图象的顶点在
为实数)图象的顶点在 轴上,求
轴上,求 的值.
的值.(
 )把抛物线
)把抛物线 向上平移
向上平移 个单位得到新的抛物线
个单位得到新的抛物线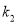 ,若
,若 ,求
,求 的图像落在
的图像落在 轴上方的部分对应的
轴上方的部分对应的 的取值范围.
的取值范围.
相关试题

