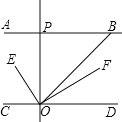
【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
参考答案:
【答案】(1)(2)(3)
【解析】根据垂直定义、角平分线的性质、直角三角形的性质求出∠POE、∠BOF、∠BOD、∠BOE、∠DOF等角的度数,即可对①②③④进行判断.
①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=![]() ∠COB=
∠COB=![]() (180﹣a)°.故①正确;
(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣![]() (180﹣a)°=
(180﹣a)°=![]() a°,
a°,
∴∠BOF=![]() ∠BOD,
∠BOD,
∴OF平分∠BOD所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=![]() a°,
a°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=![]() a°,所以④错误.
a°,所以④错误.
故答案为:①②③.
“点睛”本题考查了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补;两直线平行,同位角相等.解答此题要注意将垂直、平行、角平分线的定义结合应用,弄清图中线段和角的关系,再进行解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中既是轴对称图形又是中心对称图形的是( )
A. 正五角星 B. 等腰梯形 C. 平行四边形 D. 矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC
A(a,0)
B(3,0)
C(5,5)
△A1B1C1
A1(﹣3,2)
B1(﹣1,b)
C1(c,7)
(1)观察表中各对应点坐标的变化,并填空:a= ,b= ,c= ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
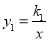 的图像与一次函数
的图像与一次函数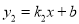 的图像交于A、B两点,A (1,n),B(
的图像交于A、B两点,A (1,n),B(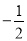 ,-2).
,-2).(1)求反比例函数和一次函数的解析式;
(2)求
 AOB的面积.
AOB的面积.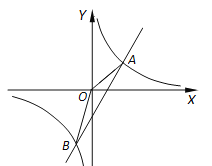
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数m,n满足m-n2=2,则代数式m2+2n2+4m-1的最小值等于______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算93﹣92﹣8×92的结果是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
相关试题

