【题目】已知△ABC在正方形网格中的位置如图所示,则点P是△ABC的( ) 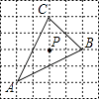
A.外心
B.内心
C.三条高线的交点
D.三条中线的交点
参考答案:
【答案】D
【解析】解:A、三角形的外心是三角形的三条垂直平分线的交点,故错误; B、三角形的内心是三角形的三条角平分线的交点,故错误;
C、三条高线的交点为三角形的垂心,故错误;
D、三角形的重心是三角形的三条中线的交点,故正确;
故选D.
【考点精析】利用三角形的“三线”和勾股定理的概念对题目进行判断即可得到答案,需要熟知1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形
 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: )
)例2 等腰三角形
 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: 或
或 或
或 )
)张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形
 中,
中, ,求
,求 的度数.
的度数.(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,
 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形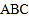 中,设
中,设 ,当
,当 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索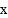 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)运用完全平方公式计算:992
(2)先化简,再求值:(2x+3y)2﹣(2x+y)(2x﹣y),其中 x=
 ,y=
,y= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若分式
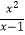 □
□ 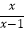 运算结果为x,则在“□”中添加的运算符号为( )
运算结果为x,则在“□”中添加的运算符号为( )
A.+
B.﹣
C.+或×
D.﹣或÷ -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小华在一起玩数字游戏,他们每人取了一张数字卡片,拼成了一个两位数. 小明说:“哇!这个两位数的十位数字与个位数字之和恰好是9.”他们又把这两张卡片对调,得到了一个新的两位数,小华说:“这个两位数恰好比原来的两位数大9.”那么,你能回答以下问题吗?
他们取出的两张卡片上的数字分别是多少?
第一次,他们拼成的两位数是多少?
第二次,他们拼成的两位数又是多少呢?请你好好动动脑筋哟!
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 D,E 在△ABC的边 BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①② 成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”.
(1)以上三个命题是真命题的为__________(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
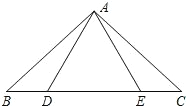
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室需要一批无盖的长方体模型,一张大纸板可以做成长方体的侧面30个,或长方体的底面25个,一个无盖的长方体由4个侧面和一个底面构成. 现有26张大纸板,则用多少张做侧面,多少张做底面才可以使得刚好配套,没有剩余?
反思:应用二元一次方程组解应用题时,要注意解题的步骤,解、设、答一个不能少,而由于未知数有两个,则必须根据题意找出两个等量关系.
相关试题

