【题目】如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s. 
(1)求PQ的长;
(2)当直线AB与⊙O相切时,求证:AB⊥PN;
(3)当t为何值时,直线AB与⊙O相切?
参考答案:
【答案】
(1)解:如图1中,连接OQ,
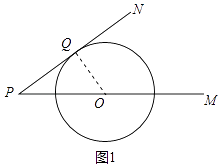
∵PN与⊙O相切于点Q,
∴OQ⊥PN,
∴∠OQP=90°,
∵OQ=6cm,OP=10cm,
∴PQ= ![]() =
= ![]() =8
=8
(2)解:如图2中,过点O作OC⊥AB于C.
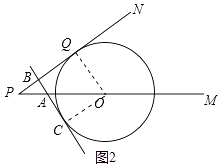
由题意,PA=5t,PB=4t,
∵OP=10,PQ=8,
∴ ![]() =
= ![]() ,∵∠P=∠P,
,∵∠P=∠P,
∴△PBA∽△PQO,
∴∠PBA=∠PQO=90°,
∴AB⊥PN
(3)解:∵∠BQO=∠CBQ=∠OCB=90°,
∴四边形OCBQ是矩形,
∴BQ=OC=6,
∵OC=6cm,
∴BQ=6cm.
①当AB运动到图2位置时,BQ=PQ﹣PB=6,
∴8﹣4t=6,
∴t=0.5s,
②当AB运动到图3位置时,

BQ=AB﹣PQ=6,
∴4t﹣8=6,
∴t=3.5s,
综上所述,t=0.5s或3.5s时,直线AB与⊙O相切
【解析】(1)连接OQ,在Rt△OPQ中,利用勾股定理即可解决问题.(2)如图2中,过点O作OC⊥AB于C.只要证明△PBA∽△PQO,即可推出∠PBA=∠PQO=90°.(3)首先证明四边形OCBQ是矩形,分两种情形列出方程即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+2的图象与反比例函数y=
 的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点,
的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点, 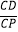 =
=  ,且S△ADP=6.
,且S△ADP=6. 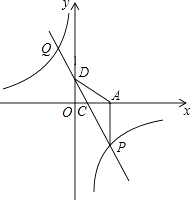
(1)求点D坐标;
(2)求一次函数和反比例函数的表达式;
(3)根据图象直接写出一次函数值小于反比例函数值时,自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0,
 ).
).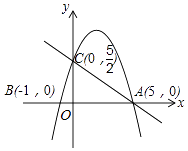
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点G的坐标.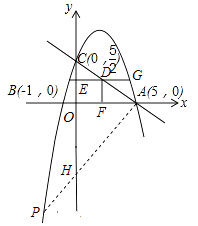
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4
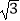 ,则S阴影=( )
,则S阴影=( ) 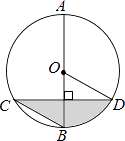
A.2π??
B. π??
π??
C. π??
π??
D. π
π
相关试题

