搜索
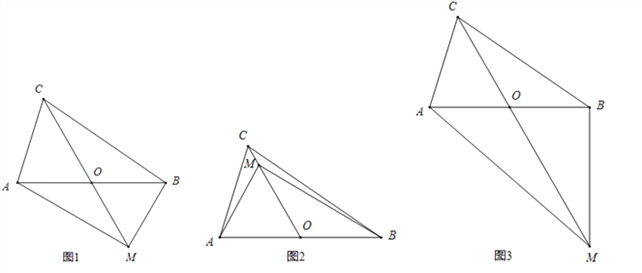
【题目】如图，在△ABC中，AB=BC=8，AO=BO，点M是射线CO上的一个动点，∠AOC=60°，则当△ABM为直角三角形时，AM的长为____________．
参考答案：
【答案】4
或4
或4
【解析】试题解析：如图1，当∠AMB=90°时，∵O是AB的中点，AB=8，∴OM=OB=4，又∵∠AOC=∠BOM=60°，∴△BOM是等边三角形，∴BM=BO=4，∴Rt△ABM中，AM=
=
；
如图2，当∠AMB=90°时，∵O是AB的中点，AB=8，∴OM=OA=4，又∵∠AOC=60°，∴△AOM是等边三角形，∴AM=AO=4；
如图3，当∠ABM=90°时，∵∠BOM=∠AOC=60°，∴∠BMO=30°，∴MO=2BO=2×4=8，∴Rt△BOM中，BM=
=，∴Rt△ABM中，AM=
=
．
综上所述，当△ABM为直角三角形时，AM的长为或或4．故答案为：或或4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】中央电视台举办的“2016年春节联欢晚会”受到广泛关注，某民间组织就2016年春节联欢晚会节目的喜爱程度，在丽州广场进行了问卷调查，并将问卷调查结果分为“非常喜欢”“比较喜欢”“感觉一般”“不太喜欢”四个等级，分别记作A，B，C，D，根据调查结果绘制出如图所示的“扇形统计图”和“条形统计图”，请结合图中所给信息解答下列问题：
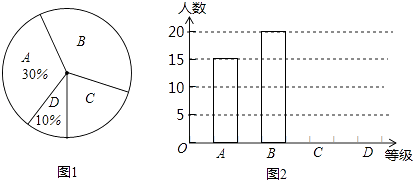
（1）这次被调查对象共有人，被调查者“不太喜欢”有人；
（2）补全扇形统计图和条形统计图；
（3）在“非常喜欢”调查结果里有5人为80后，分别为3男2女，在这5人中，该民间组织打算随机抽取2人进行采访，请你用列表法或列举法求出所选2人均为男生的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】节能电动车越来越受到人们的喜欢，新开发的各种品牌电动车相继投入市场．小李车行经营的A型节能电动车2015年销售总额为m万元，2016年每辆A型节能电动车的销售价比2015年降低2000年，若2015年和2016年卖出的节能电动车的数量相同（同一型号的节能电动车每辆的销售价格相同），则2016年的销售总额比2015年减少20%．
（1）2016年A型节能电动车每辆售价多少万元？（用列方程方法解答）
（2）小李车行计划端午节后新购进一批A型节能电动车和新型B型节能电动车，每购进3辆节能电动车，批发商就给车行返回1500元．若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍，全部销售获得的利润不少于18万元，且2016年A，B两种型号节能电动车的进货和销售价格如表，那么2016年新款B型节能电动车至少要购进多少辆？A型节能电动车
B型节能电动车
进货价格（万元/辆）
0.55
0.7
销售价格（万元/辆）
2016年的销售价格
2
-
科目： 来源： 题型：
查看答案和解析>>【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°，已知A点的高度AB为2米，台阶AC的坡度i=1：2，且B，C，E三点在同一条直线上，请根据以上条件求出树DE的高度．（测倾器的高度忽略不计，结果保留根号）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+2的图象与反比例函数y=
的图象交于P、G两点，过点P作PA⊥x轴，一次函数图象分别交x轴、y轴于C、D两点， 
= 
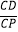，且S△ADP=6．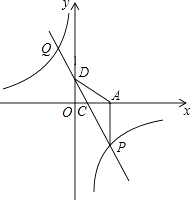 
（1）求点D坐标；
（2）求一次函数和反比例函数的表达式；
（3）根据图象直接写出一次函数值小于反比例函数值时，自变量x的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知⊙O的半径为6cm，射线PM经过点O，OP=10cm，射线PN与⊙O相切于点Q．A、B两点同时从点P出发，点A以5cm/s的速度沿射线PM方向运动，点B以4cm/s的速度沿射线PN方向运动，设运动时间为t s．
（1）求PQ的长；
（2）当直线AB与⊙O相切时，求证：AB⊥PN；
（3）当t为何值时，直线AB与⊙O相切？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c与x轴交于A（5，0），B（﹣1，0）两点，与y轴交于点C（0，
）．
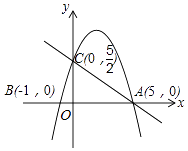
（1）求抛物线的解析式；
（2）在抛物线上是否存在点P，使得△ACP是以点A为直角顶点的直角三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由；
（3）点G为抛物线上的一动点，过点G作GE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线，垂足为点F，连接EF，当线段EF的长度最短时，求出点G的坐标．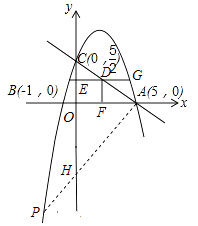
相关试题
