【题目】如图,一次函数y=kx+2的图象与反比例函数y= ![]() 的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点,
的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点, ![]() =
= ![]() ,且S△ADP=6.
,且S△ADP=6. 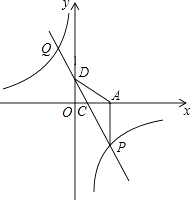
(1)求点D坐标;
(2)求一次函数和反比例函数的表达式;
(3)根据图象直接写出一次函数值小于反比例函数值时,自变量x的取值范围.
参考答案:
【答案】
(1)解:对于y=kx+2,令x=0,得到y=2,即D(0,2)
(2)解:∵AP∥y轴,∴ ![]() =
= ![]() =
= ![]() ,
,
∵OD=2,∴AP=4,
∵S△ADP= ![]() APOA=6,
APOA=6,
∴OA=3,即P(3,﹣4),
把P坐标代入反比例解析式得:m=﹣12,
∴反比例函数解析式为y=﹣ ![]() ,
,
把P坐标代入y=kx+2中得:﹣4=3k+2,即k=﹣2,
∴一次函数解析式为y=﹣2x+2
(3)解:联立得: 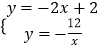 ,
,
解得: ![]() 或
或 ![]() ,
,
∴Q(﹣2,6),P(3,﹣4),
则由图象得:当x>3或﹣2<x<0时,一次函数值小于反比例函数值
【解析】(1)对于一次函数,令x=0求出y的值,即可确定出D坐标;(2)由AP与y轴平行,得比例,根据OD的长求出AP的长,由三角形ADP面积求出OA的长,确定出P坐标,代入反比例解析式求出m的值,代入一次函数求出k的值,即可确定出各自的解析式;(3)联立一次函数与反比例函数解析式求出交点坐标,确定出G坐标,利用图象确定出一次函数值小于反比例函数值时x的范围即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】节能电动车越来越受到人们的喜欢,新开发的各种品牌电动车相继投入市场.小李车行经营的A型节能电动车2015年销售总额为m万元,2016年每辆A型节能电动车的销售价比2015年降低2000年,若2015年和2016年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则2016年的销售总额比2015年减少20%.
(1)2016年A型节能电动车每辆售价多少万元?(用列方程方法解答)
(2)小李车行计划端午节后新购进一批A型节能电动车和新型B型节能电动车,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且2016年A,B两种型号节能电动车的进货和销售价格如表,那么2016年新款B型节能电动车至少要购进多少辆?A型节能电动车
B型节能电动车
进货价格(万元/辆)
0.55
0.7
销售价格(万元/辆)
2016年的销售价格
2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.

(1)求PQ的长;
(2)当直线AB与⊙O相切时,求证:AB⊥PN;
(3)当t为何值时,直线AB与⊙O相切? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0,
 ).
).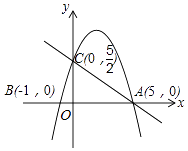
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点G的坐标.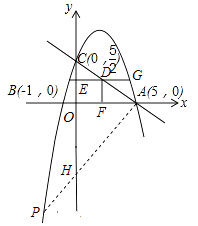
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.

相关试题

