【题目】如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ![]() ,则S阴影=( )
,则S阴影=( ) 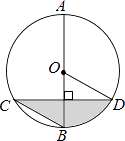
A.2π??
B.![]() π??
π??
C.![]() π??
π??
D.![]() π
π
参考答案:
【答案】B
【解析】解:如图,假设线段CD、AB交于点E, 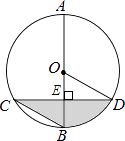
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2 ![]() ,
,
又∵∠BCD=30°,
∴∠DOE=2∠BCD=60°,∠ODE=30°,
∴OE=DEcot60°=2 ![]() ×
× ![]() =2,OD=2OE=4,
=2,OD=2OE=4,
∴S阴影=S扇形ODB﹣S△DOE+S△BEC= ![]() ﹣
﹣ ![]() OE×DE+
OE×DE+ ![]() BECE=
BECE= ![]() ﹣2
﹣2 ![]() +2
+2 ![]() =
= ![]() .
.
故选B.
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.

(1)求PQ的长;
(2)当直线AB与⊙O相切时,求证:AB⊥PN;
(3)当t为何值时,直线AB与⊙O相切? -
科目: 来源: 题型:
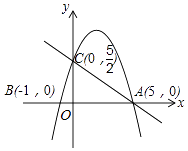
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0,
 ).
).
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点G的坐标.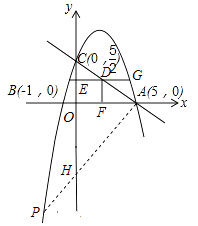
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论: ①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )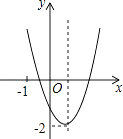
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】为节约用电,某市根据每户居民每月用电量分为三档收费.第一档电价:每月用电量低于240度,每度0.4883元;第二档电价:每月用电量为240~400度,每度0.5383元;第三档电价:每月用电量为不低于400度,每度0.7883元.小灿同学对该市有1000户居民的某小区居民月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )

A. 本次抽样调查的样本容量为50 B. 估计该小区按第一档电价交费的居民户数最多
C. 该小区按第二档电价交费的居民有220户 D. 该小区按第三档电价交费的居民比例约为6%
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为(-2,-2),(3,1),(0,2),若把三角形ABC向上平移 3 个单位长度,再向左平移
 个单位长度得到三角形
个单位长度得到三角形  ,点A,B,C的对应点分别为
,点A,B,C的对应点分别为  ,
, ,
, .
.(1)写出点
 ,
, ,
, 的坐标;
的坐标;(2)在图中画出平移后的三角形
 ;
;(3)三角形
 的面积为__________.
的面积为__________.
相关试题

