【题目】

(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
参考答案:
【答案】(1)甲、乙3.4秒后相遇;(2)甲出发2或5秒后,甲到A、B、C三点的距离和为40个单位;(3)﹣44.
【解析】试题分析:(1)可设x秒后甲与乙相遇,根据相遇时甲与乙所行路程之和为34列出方程,求解即可;
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,分甲应为于AB或BC之间两种情况讨论即可求解;
(3)设z秒后甲、乙在数轴上再次相遇,那么此时甲、乙表示在数轴上为同一点,依此列出方程求解即可.
解:(1)设x秒后甲与乙相遇,则
4x+6x=34,
解得x=3.4,
答:甲、乙3.4秒后相遇;
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.
①AB之间时:4y+(14﹣4y)+(14﹣4y+20)=40,解得y=2;
②BC之间时:4y+(4y﹣14)+(34﹣4y)=40,解得y=5.
答:甲出发2或5秒后,甲到A、B、C三点的距离和为40个单位;
(3)①甲从A向右运动2秒时返回,设z秒后与乙再次相遇.此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为:﹣24+4×2﹣4z;乙表示的数为:10﹣6×2﹣6z,
依据题意得:﹣24+4×2﹣4z=10﹣6×2﹣6z,
解得:z=7,
相遇点表示的数为:﹣24+4×2﹣4z=﹣44(或:10﹣6×2﹣6z=﹣44),
②甲从A向右运动5秒时返回,设y秒后与乙相遇.
甲表示的数为:﹣24+4×5﹣4z;乙表示的数为:10﹣6×5﹣6z,
依据题意得:﹣24+4×5﹣4z=10﹣6×5﹣6z,
解得:z=﹣8(不合题意舍去),
答:当甲、乙在数轴上再次相遇时,相遇点表示的数为﹣44.
故答案为﹣44.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
第一次
第二次
第三次
第四次
第五次
第六次
第七次
-3
+7
-9
+8
+6
-5
-4
(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节将至,某移动公司计划推出两种新的计费方式,如下表所示:
方式1
方式2
月租费
30元/月
0
本地通话费
0.20元/分钟
0.40元/分钟
请解决以下两个问题:(通话时间为正整数)
(1)若本地通话100分钟,按方式一需交费多少元?按方式二需交费多少元?
(2)对于某月本地通话,当通话多长时间时,按两种计费方式的收费一样多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
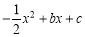 交x轴于点A、B,交y轴于点C,点A的坐标是(-1,0),点C的坐标是(0,2).
交x轴于点A、B,交y轴于点C,点A的坐标是(-1,0),点C的坐标是(0,2).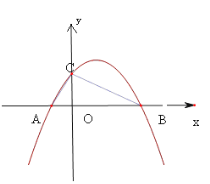
(1)求该抛物线的解析式。
(2)已知点P是抛物线上的一个动点,点N在x轴上。
①若点P在x轴上方,且△APN是等腰直角三角形,求点N的坐标;
②若点P在x轴下方,且△APN∽△BOC,请直接写出点N的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC。
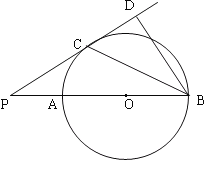
求证:(1)BC平分∠PBD;
(2)BC2=AB·BD。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC,垂足为D.CD=1,AD=2,BD=4.
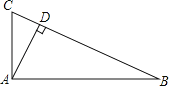
(1)求∠BAC的度数?并说明理由;
(2)P是边BC上一点,连结AP,当△ACP为等腰三角形时,求CP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
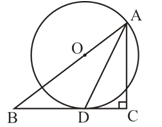
(1)求证:BC是⊙O切线;
(2)若BD=5, DC=3,求AC的长。
相关试题

