【题目】如图,AD⊥BC,垂足为D.CD=1,AD=2,BD=4.
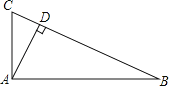
(1)求∠BAC的度数?并说明理由;
(2)P是边BC上一点,连结AP,当△ACP为等腰三角形时,求CP的长.
参考答案:
【答案】(1)∠BAC=90°;(2)CP的长为2或![]() 或2.5.
或2.5.
【解析】
试题分析:首先由勾股定理求出AC和AB,再由勾股定理逆定理证出△ABC为直角三角形得出∠BAC=90°;当△ACP为等腰三角形时,CP有三个解.
解:(1)∠BAC=90°;理由:
∵AD⊥BC,
∴∠ADC=∠ADB=90°;
由勾股定理可得 AC2=AD2+CD2=12+22=5,AB2=AD2+BD2=22+42=20;
∴AC2+AB2=25;
∵BC2=(BD+CD)2=52=25;
∴AC2+AB2=BC2;
∴△ABC是直角三角形;
∴∠BAC=90°;
(2)当△ACP为等腰三角形时,有三种情况:
①当AC=AP时,CP=2CD=2;
②当AC=CP时,∵AC=![]() ,∴CP=
,∴CP=![]() ;
;
③当CP=AP时,CP=![]() =2.5;
=2.5;
因此,当△ACP为等腰三角形时,CP的长为2或![]() 或2.5.
或2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
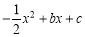 交x轴于点A、B,交y轴于点C,点A的坐标是(-1,0),点C的坐标是(0,2).
交x轴于点A、B,交y轴于点C,点A的坐标是(-1,0),点C的坐标是(0,2).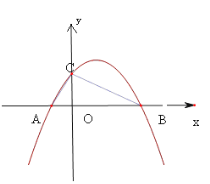
(1)求该抛物线的解析式。
(2)已知点P是抛物线上的一个动点,点N在x轴上。
①若点P在x轴上方,且△APN是等腰直角三角形,求点N的坐标;
②若点P在x轴下方,且△APN∽△BOC,请直接写出点N的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC。
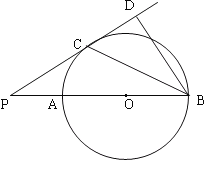
求证:(1)BC平分∠PBD;
(2)BC2=AB·BD。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
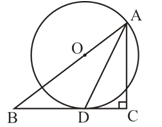
(1)求证:BC是⊙O切线;
(2)若BD=5, DC=3,求AC的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.小华同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小丽同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).

(1)你能说出小华、小丽所折出的菱形的理由吗?
(2)请你通过计算,比较小华和小丽同学的折法中,哪种菱形面积较大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
相关试题

