【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
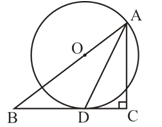
(1)求证:BC是⊙O切线;
(2)若BD=5, DC=3,求AC的长。
参考答案:
【答案】(1)见解析证明;(2)见解析证明.
【解析】
试题分析:(1)要证BC是⊙O的切线,只要连接OD,再证OD⊥BC即可;(2)过点D作DE⊥AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∽△BAC,根据相似三角形的性质得出AC的长.
试题解析:(1)证明: 如图1,连接OD.∵ OA=OD, AD平分∠BAC,∴ ∠ODA=∠OAD, ∠OAD=∠CAD,∴ ∠ODA=∠CAD,∴ OD//AC,∴ ∠ODB=∠C=90,∴ BC是⊙O的切线;

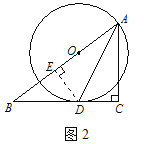
(2) 如图2,过D作DE⊥AB于E.∴ ∠AED=∠C=90,又∵ AD=AD, ∠EAD=∠CAD, ∴ △AED≌△ACD.
∴ AE=AC, DE=DC=3,在Rt△BED中,∠BED =90,由勾股定理,得BE=![]() .设AC=x(x>0), 则AE=x,在Rt△ABC中,∠C=90, BC=BD+DC=8, AB=x+4, 由勾股定理,得
.设AC=x(x>0), 则AE=x,在Rt△ABC中,∠C=90, BC=BD+DC=8, AB=x+4, 由勾股定理,得![]() ,
,
解得x=6,即 AC=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC。
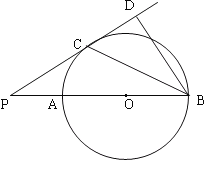
求证:(1)BC平分∠PBD;
(2)BC2=AB·BD。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC,垂足为D.CD=1,AD=2,BD=4.
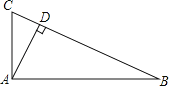
(1)求∠BAC的度数?并说明理由;
(2)P是边BC上一点,连结AP,当△ACP为等腰三角形时,求CP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.小华同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小丽同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).

(1)你能说出小华、小丽所折出的菱形的理由吗?
(2)请你通过计算,比较小华和小丽同学的折法中,哪种菱形面积较大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正多边形的一个外角为30°,那么这个正多边形的边数是( )
A. 6 B. 11 C. 12 D. 18
相关试题

