【题目】如图,在矩形ABCD中,AB=8,BC=12,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为 . 
参考答案:
【答案】10或12
【解析】解:如图,在矩形ABCD中,AB=CD=8,BC=AD=12.
如图1,当PB=PC时,点P是BC的中垂线与AD的交点,则AP=DP= ![]() AD=6.
AD=6.
在Rt△ABP中,由勾股定理得 PB= ![]() =
= ![]() =10;
=10;
如图2,当BP=BC=12时,△BPC也是以PB为腰的等腰三角形.
综上所述,PB的长度是10或12.
所以答案是:10或12.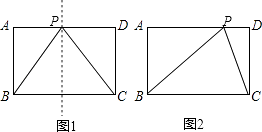
【考点精析】本题主要考查了等腰三角形的性质和勾股定理的概念的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上与原点的距离小于8的点对应的x满足( )
A. ﹣8<x<8 B. x<﹣8或x>8 C. x<8 D. x>8
-
科目: 来源: 题型:
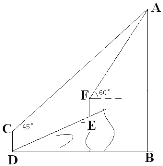
查看答案和解析>>【题目】如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)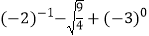
(2)(﹣x6)﹣(﹣3x3)2﹣[﹣(2x)2]3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组):
(1)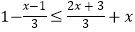
(2)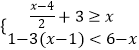 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
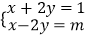 .
.
(1)求这个方程组的解;
(2)当m取何值时,这个方程组的解中,x大于1,y不小于﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,有矩形AOBC,点A、B的坐标分别为(0,4)、(10,0),点P的坐标为(2,0),点M在线段AO上,点N在线段AC上,总有∠MPN=90 ,点M从点O运动到点A,当点M运动到A点时,点N与点C重合(如图2)。令AM=x
(1).直接写出点C的坐标___________;
(2)、①设MN2=y,请写出y关于x的函数关系式,并求出y的最小值;
②连接AP交MN于点D,若MN⊥A P,求x的值;
(3)、当点M在边AO上运动时,∠PMN的大小是否发生变化?请说明理由.
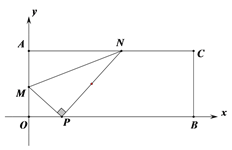
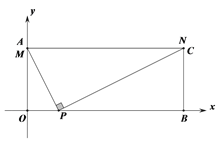
图1 图2
相关试题

