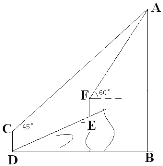
【题目】如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
参考答案:
【答案】10![]() +11.5
+11.5
【解析】作C′M⊥AB于M,MC′的延长线与DC的延长线交于N,作CG⊥AB于G,D′F⊥CD于F,设AM为xm,解Rt△AC′M与Rt△DD′F,用含x的代数式表示出AG、CG,然后根据△ACG是等腰直角三角形得出AG=CG,依此列出方程,解方程即可求出AM,结合图形计算即可.
解:R⊥AB, FH⊥AB 延长FE交DB于点G

设BG=x
由题意可得,ER=FH=BG=x
HR=10,AH=![]() x,AR=
x,AR=![]() x+10
x+10
CR=10![]() +X
+X
∴10![]() +X=
+X=![]() x+10
x+10
解得x=10
∴AB=10![]() +11.5
+11.5
“点睛”此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市最高气温是33℃,最低气温是24℃,则该市气温t(℃)的变化范围是()
A. t>33 B. t≤24 C. 24<t<33 D. 24≤t≤33
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上与原点的距离小于8的点对应的x满足( )
A. ﹣8<x<8 B. x<﹣8或x>8 C. x<8 D. x>8
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)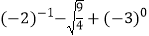
(2)(﹣x6)﹣(﹣3x3)2﹣[﹣(2x)2]3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=12,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组):
(1)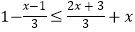
(2)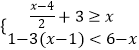 .
.
相关试题

