搜索
【题目】如图，四边形ABCD中，∠ADB＝60°，∠CDB＝50°．
（1）若AD∥BC，AB∥CD，求∠ABC的度数；
（2）若∠A＝70°，请写出图中平行的线段，并说明理由．
参考答案：
【答案】（1）110°;（2）AB∥CD．理由见解析.
【解析】
（1）先由平行线的性质求得∠A，再由平行线的性质求得∠ABC；
（2）根据三角形内角和定理可求∠ABD＝50°，再由平行线的判定即可求解．
解：（1）∵∠ADB＝60°，∠CDB＝50°，
∴∠ADC＝110°
∵AD∥BC，
∴∠A＝70°，
∵AB∥CD，
∴∠ABC＝110°；
（2）AB∥CD．理由如下：
∵∠ADB＝60°，∠A＝70°，
∴∠ABD＝50°，
∴∠CDB＝∠ABD＝50°，
∴AB∥CD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校九年级两个班，各选派10名学生参加学校举行的“汉字听写”大赛预赛，各参赛选手的成绩如下：
九(1)班：88，91，92，93，93，93，94，98，98，100；
九(2)班：89，93，93，93，95，96，96，98，98，99．
通过整理，得到数据分析表如下：
班级
最高分
平均分
中位数
众数
方差
九(1)班
100
m
93
93
12
九(2)班
99
95
n
p
8.4
(1)直接写出表中m、n、p的值为：m=______，n=______，p=______；
(2)依据数据分析表，有人说：“最高分在(1)班，(1)班的成绩比(2)班好．”但也有人说(2)班的成绩要好．请给出两条支持九(2)班成绩更好的理由；
(3)学校确定了一个标准成绩，等于或大于这个成绩的学生被评定为“优秀”等级，如果九(2)班有一半的学生能够达到“优秀”等级，你认为标准成绩应定为______分，请简要说明理由．
-
科目： 来源： 题型：
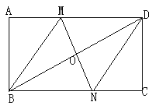
查看答案和解析>>【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点N，连接BM，DN.
（1）求证：四边形BMDN是菱形；
（2）若AB=4，AD=8，求MD的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】用大小相等的小正方形按一定规律拼成下列图形.
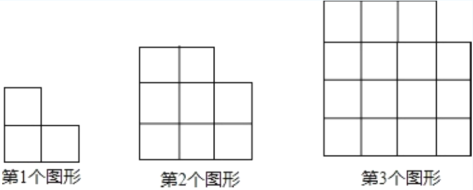
⑴第4个图形中小正方形的个数是______；
⑵第
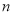个图形中小正方形的个数是多少？ -
科目： 来源： 题型：
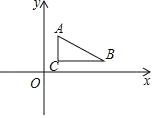
查看答案和解析>>【题目】已知，如图，A点坐标是(1，3)，B点坐标是(5，1)，C点坐标是(1，1)
(1)求△ABC的面积是____；
(2)求直线AB的表达式；
(3)一次函数y＝kx+2与线段AB有公共点，求k的取值范围；
(4)y轴上有一点P且△ABP与△ABC面积相等，则P点坐标是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店出售A、B两种商品，一月份这两种商品的利润都是10万元，后因某种原因确定增加出售A种商品的数量，使A种商品每月利润的增长率都为a，同时减少B种商品的数量，使B种商品每月利润减少的百分率也都是a，（1）分别求出二月份出售A和B两种商品的利润是多少万元？（2）求出三月份出售A、B两种商品的总利润是多少万元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的文字后，回答问题：
甲、乙两人同时解答题目：“化简并求值：
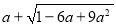，其中a=5．”甲、乙两人的解答不同；甲的解答是：
；乙的解答是：
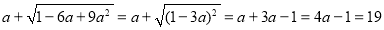．（1） 的解答是错误的．
（2）错误的解答在于未能正确运用二次根式的性质： ．
（3）模仿上题解答：化简并求值：
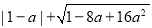，其中a=2．
相关试题
