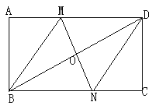
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
参考答案:
【答案】(1)见解析;(2)MD长为5.
【解析】
(1)根据矩形性质求出AD∥BC,推出∠MDO=∠NBO,∠DMO=∠BNO,证△DMO≌△BNO,推出OM=ON,得出平行四边形BMDN,推出菱形BMDN;
(2)根据菱形性质求出DM=BM,在Rt△AMB中,根据勾股定理得出BM2=AM2+AB2,即可列方程求得.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中,
∠DMO=∠BNO,∠MDO=∠NBO,OB=OD,
∴△DMO≌△BNO(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)∵四边形BMDN是菱形,∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8-x)2+42,
解得:x=5,
答:MD长为5.
故答案为:(1)见解析;(2)MD长为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在一个长方形广场的四角都设计一块半径相同的四分之一圆形的花坛.若广场的长为m米,宽为n米,圆形的半径为r米.
(1)列式表示广场空地的面积.
(2)若广场的长为300米,宽为200米,圆形的半径为30米,求广场空地的面积(计算结果保留π).
(3)如图2所示,在(2)的条件下,若在广场的中间再建一个半径为R的圆形花坛,使广场的空地面积不少于广场总面积的
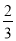 ,求R的最大整数值(π取3.1).
,求R的最大整数值(π取3.1).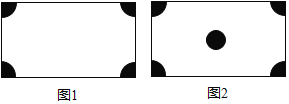
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,现有一张边长为4的正方形纸片
 ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100;
九(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级
最高分
平均分
中位数
众数
方差
九(1)班
100
m
93
93
12
九(2)班
99
95
n
p
8.4
(1)直接写出表中m、n、p的值为:m=______,n=______,p=______;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好.”但也有人说(2)班的成绩要好.请给出两条支持九(2)班成绩更好的理由;
(3)学校确定了一个标准成绩,等于或大于这个成绩的学生被评定为“优秀”等级,如果九(2)班有一半的学生能够达到“优秀”等级,你认为标准成绩应定为______分,请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用大小相等的小正方形按一定规律拼成下列图形.
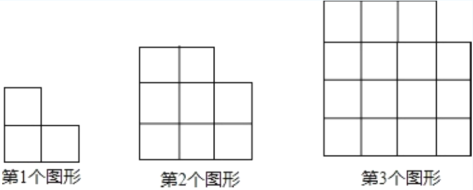
⑴第4个图形中小正方形的个数是______;
⑵第
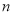 个图形中小正方形的个数是多少?
个图形中小正方形的个数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠ADB=60°,∠CDB=50°.
(1)若AD∥BC,AB∥CD,求∠ABC的度数;
(2)若∠A=70°,请写出图中平行的线段,并说明理由.

-
科目: 来源: 题型:
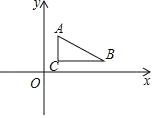
查看答案和解析>>【题目】已知,如图,A点坐标是(1,3),B点坐标是(5,1),C点坐标是(1,1)
(1)求△ABC的面积是____;
(2)求直线AB的表达式;
(3)一次函数y=kx+2与线段AB有公共点,求k的取值范围;
(4)y轴上有一点P且△ABP与△ABC面积相等,则P点坐标是_____.
相关试题

