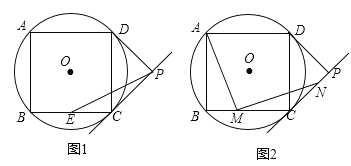
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
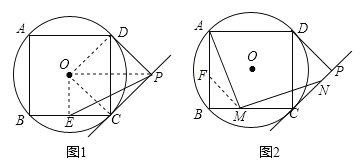
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
参考答案:
【答案】(1)2![]() ;(2)2
;(2)2![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题(1)由切线的性质和正方形的判定与性质得出⊙O的半径即可;
(2)由垂径定理得出OE⊥BC,∠OCE=45°,再用勾股定理即可得出结论;
(3)在AB上截取BF=BM,利用(1)中所求,得出∠ECP=135°,再利用全等三角形的判定与性质得出即可.
试题解析:(1)如图1,连接OD,OC,∵PC、PD是⊙O的两条切线,C、D为切点,∴∠ODP=∠OCP=90°,∵四边形ABCD是⊙O的内接正方形,∴∠DOC=90°,OD=OC,∴四边形DOCP是正方形,∵AB=4,∠ODC=∠OCD=45°,∴DO=CO=DCsin45°=![]() ×4=
×4=![]() ;
;
(2)如图1,连接EO,OP,∵点E是BC的中点,∴OE⊥BC,∠OCE=45°,则∠E0P=90°,∴EO=EC=2,OP=![]() CO=4,∴PE=
CO=4,∴PE=![]() =
=![]() ;
;
(3)如图2,在AB上截取BF=BM,∵AB=BC,BF=BM,∴AF=MC,∠BFM=∠BMF=45°,∵∠AMN=90°,∴∠AMF+∠NMC=45°,∠FAM+∠AMF=45°,∴∠FAM=∠NMC,∵由(1)得:PD=PC,∠DPC=90°,∴∠DCP=45°,∴∠MCN=135°,∵∠AFM=180°﹣∠BFM=135°,在△AFM和△CMN中,∵∠FAM=∠CMN,AF=MC,∠AFM=∠MCN,∴△AFM≌△CMN(ASA),∴AM=MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
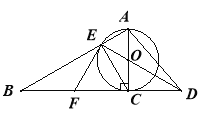
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=
 ,tanB=
,tanB= .半径为2的⊙C, 分别交AC、BC于点D、E,得到
.半径为2的⊙C, 分别交AC、BC于点D、E,得到 .
.(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如,三点坐标分别为A(0,3),B(-3,4),C(1,-2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(-2,-1),F(3,m)三点的“矩面积”为20,则m的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据直尺和三角尺的实物摆放图,解决下列问题.



(1)如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是__________;
(2)如图2,图中互余的角有________________,若要使直尺的边缘DE与三角尺的AB边平行,则应满足_________(填角相等);
(3)如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市实验中学学生会准备调查七年级学生参加“球类”“书画类”“棋牌类:”“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时,我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.这三位同学的调查方式中,最合理的是______(填“甲”“乙”或“丙”)同学的调查方式.
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图,请你根据图表提供的信息解答下列问题:
①a=________,b=________;
②在扇形统计图中,器乐类所对应的圆心角的度数是________;
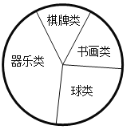
③若该校七年级有学生660人,请你估计大约有多少学生参加球类校本课程?
类别
频数(人数)
百分比
球类
25
书画类
20
20%
棋牌类
15
b
器乐类
合计
a
100%
相关试题

