【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据原命题和逆命题的关系,即调换条件和结论;
(2)根据(1)的条件和结论写出已知和求证,再画出图形,然后结合图形证明Rt△AEBE≌RtADC,证得AB=AC,即为等腰三角形.
解:(1)逆命题是如果一个三角形两条边上的高相等,那么这个三角形是等腰三角形;;
(2)已知:在△ABC中,CD⊥AB,BE⊥AC,且CD=BE,
求证:△ABC是等腰三角形.
证明:如图,
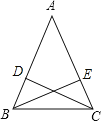
∵BE、CD是△ABC的高,
∴CD⊥AB,BE⊥AC,
∵∠A=∠A,
∵BE=CD,
∴Rt△AEB≌Rt△ADC(AAS),
∴AB=AC,
∴△ABC是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直角三角形ABC沿斜边BC所在直线向右平移一定的长度得到三角形DEF,DE交AC于G,连接AE和AD.有下列结论:①AC∥DF;②AD∥BE,AD=BE;③∠B=∠DEF;④ED⊥AC.其中正确的结论有( )

A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
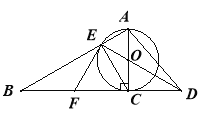
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=
 ,tanB=
,tanB= .半径为2的⊙C, 分别交AC、BC于点D、E,得到
.半径为2的⊙C, 分别交AC、BC于点D、E,得到 .
.(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.

-
科目: 来源: 题型:
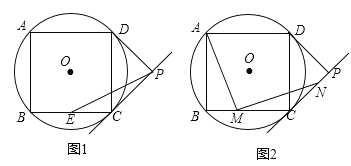
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如,三点坐标分别为A(0,3),B(-3,4),C(1,-2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(-2,-1),F(3,m)三点的“矩面积”为20,则m的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据直尺和三角尺的实物摆放图,解决下列问题.



(1)如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是__________;
(2)如图2,图中互余的角有________________,若要使直尺的边缘DE与三角尺的AB边平行,则应满足_________(填角相等);
(3)如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.
相关试题

