A.B₂=A(10%～20%)                     B.A=F+B₁+C₁+D₁+E₁

C.A-(B₁+B₃)=C₁+C₂+C₃                 D.C₃=B₂(80%～90%)

D.抗“莠去净”基因的遗传具有母系遗传的特性，且杂交后代不会出现性状分离
5、下图为生态系统能量流动示意图，下列等式中错误的是

4、1970年以前，未发现植物对除草剂有抗性，但到1985年则发现48种植物至少对一种除草剂产生了抗性。抗药性的产生和扩展越来越受到社会各方面的重视。下表是苋菜叶绿体基因pbsA抗“莠去净”(一种除草剂)品系和敏感品系的部分DNA碱基序列和氨基酸序列。下列说法错误的是:

抗

GCT丙氨酸

GGT甘氨酸

TTC苯丙氨酸

AAC天冬氨酸

敏感

GCA丙氨酸

AGT丝氨酸

TTC苯丙氨酸

AAC天冬氨酸

氨基酸位置

227

228

229

230

A.由上表可推知，核苷酸代换速率比氨基酸代换速率要快

B.苋菜能抗除草剂，是由于基因突变导致了第228位上的氨基酸发生了改变

C.苋菜抗“莠去净”品系能在种群中快速扩展，其遗传学原理是抗性基因在叶绿体中能自我复制，并通过细胞质遗传方式扩展

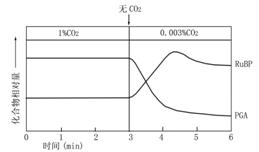
3、用同位素示踪法研究光合作用，植物先在1%CO₂中进行光合作用，而后将CO₂浓度降到0.003%。测得¹⁴C标记的3－磷酸甘油酸(PGA，含3个碳原子的化合物)和核酮糖二磷酸(RuBP，含5个碳原子的化合物)含量的变化如右图所示。从这项研究中能得出的结论有:

①RuBP可能是CO₂受体，因为当CO₂浓度突然降低，作为CO₂受体的化合物会积累，而在高浓度CO₂时它的含量下降。

②PGA是光合初产物，因为在高浓度CO₂时它的含量上升，而当CO₂浓度突然降低，它的含量减少。

③RuBP可由PGA转变来，否则在PGA含量下降时RuBP的含量不会增加。

A.只有①          B.只有①②     C.只有②③     D.都正确

D.B和C都正确

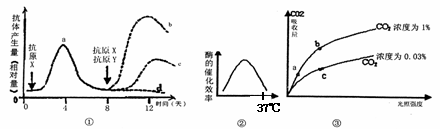
A.图①表示将抗原注射于兔体内后抗体产生量的变化，当第8天，同时注射抗原Y和X，则曲线b、c分别表示对抗原Y和X的抗体产生量

B.图②表示温度与唾液淀粉酶的催化效率的关系

C.图③表示将植物放在不同浓度CO₂环境条件下，其光合速率受光照强度影响的变化曲线，图中b点与a点相比较，b点处叶肉细胞中C₃的含量较低；b点与c点相比较，b点处叶肉细胞中C₃的含量较高

2、关于下面三个曲线图的叙述中，正确的是

1、下列相关实验的说法正确的是

A.抗虫棉的培育使用了体细胞杂交技术、植物组织培养技术和基因重组技术

B.鉴定脂肪存在，观察细胞质的流动和洋葱根尖细胞的有丝分裂都需要用到高倍显微镜

C.观察SO₂对植物的影响可使用黄瓜幼苗，是因为黄瓜幼苗对SO₂反应敏感

D.能用双缩脲试剂检测出某肾炎患者的尿液中是否含蛋白质

21．（本小题满分14分）

解：（１）依题意设双曲线C的方程为：，点P代入得．

所以双曲线C 的方程是．……………………………………………… 4分

（２）依题意，直线的方程为（）， ……………………………… 5分

设为双曲线右支上满足的点，

则到直线的距离等于1，即．……………………… 6分

①若，则直线与双曲线右支相交，

故双曲线的右支上有两个点到直线的距离等于1，与题意矛盾．……………… 8分

②若（如图所示），则直线在双曲线的右支的上方，故，

从而有．

又因为，所以有，

整理，得．……（★） ………10分

（i）若，则由（★）得，，

即． ……………………………………………………………………………12分

（ii）若，则方程（★）必有相等的两个实数根，故由

，

解之得（不合题意，舍去），此时有

，，即．

      综上所述，符合条件的的值有两个：

，此时；，此时．  ………………………………14分

20．（本小题满分14分）

解：（１）由题意得0对一切∈[-3,-2 ）恒成立，

即2-0对一切∈[-3,-2 ）恒成立．  ………………………………… 2分

∴2, =,…………………………………… 4分

当∈[-3,-2 ）时， -（-）²+<-（2-）²+=-6，

∴>- .        …………………………………………………… 6分

∴，所以的取值范围是（-∞，-].   ………………………………… 7分

（２）因为=2-[2(1-)+ ]，

当时，则为单调递减函数，没有最大值． …………………………… 9分

当>0时,  ∵<1    ∴2(1-)>0 ,>0,

∴. ………………………………………………………………11分

由2(1-)+ 得=1 由于=1+>1，舍去．

所以当=1-时，．……………………………………13分

令2-2=1-2，解得=或=-2，即为所求． …………………14分