21.(本题满分14分
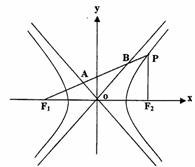
如图,设F1,F2分别是双曲线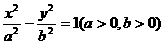 的左、右焦点,P为双曲线上
的左、右焦点,P为双曲线上
 一点,PF2⊥F1F2,连接PF1,分别与双曲线的两渐近线交于点A,B,且
一点,PF2⊥F1F2,连接PF1,分别与双曲线的两渐近线交于点A,B,且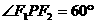 .
.
 (1)求双曲线的离心率;
(1)求双曲线的离心率;
(2)若线段AB的长度为 ,求双曲线的方程.
,求双曲线的方程.
20.(本小题满分14分)
已知函数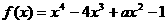 在区间[0,1]上单调递增,在区间[1,2]上单调递
在区间[0,1]上单调递增,在区间[1,2]上单调递
减.
(1)求a的值;
(2)是否存在实数b,使得函数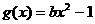 的图象与函数
的图象与函数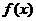 的图象恰有2个交
的图象恰有2个交
点,若存在,求出实数b的值;若不存在,试说明理由.
19.(本题满分14分)
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是梯形,AD//BC,BC=2AD,
AB⊥AC,AB=AC=2,E是BC的中点,四面体P-ABC的体积为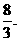
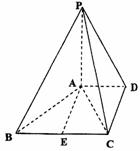 (1)求异面直线AE与PC所成的角的余弦值;
(1)求异面直线AE与PC所成的角的余弦值;
(2)求点D到平面PAB的距离;
18.(本小题满分14分)
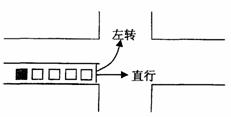 如图,一辆车要直行通过某十字路口,此时
如图,一辆车要直行通过某十字路口,此时
前方交通灯为红灯,且该车前面已有4辆车
依次在同一车道上排队等候(该车道只可以
直行或左转行驶). 已知每辆车直行的概率
是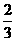 ,左转行驶的概率是
,左转行驶的概率是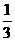 ,该路口红绿灯
,该路口红绿灯
转换间隔时间均为1分钟. 假设该车道上一
辆直行的车驶出停车线需要10秒钟,一辆左转的车驶出停车线需要20秒钟,求:
(1)前4辆车恰有2辆车左转行驶的概率;
(2)该车在第一次绿灯这亮起时的1分钟内通过该路口的概率(汽车驶出停车线就算通
过路口)
15.给出下列四个命题中:YCY
①a,b,c为三个平面向量,若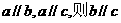 ;
;
②若函数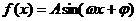 的图象关于直线
的图象关于直线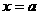 对称,则当
对称,则当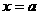 时
时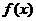 必取最
必取最
大值;
③若函数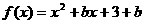 是偶函数,则
是偶函数,则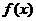 的最小值为3;
的最小值为3;
④函数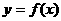 的图象与直线
的图象与直线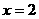 的交点个数是0个或1个.
的交点个数是0个或1个.
其中正确的命题的序号是 .

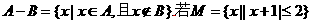 ,
,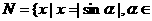 R},则M-N=( )
R},则M-N=( ) 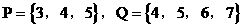 ,定义P※Q=
,定义P※Q=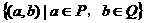 ,则P※Q中元素的个数为
( )
,则P※Q中元素的个数为
( )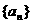 的前n项和为Sn,已知
的前n项和为Sn,已知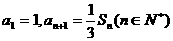 ,求
,求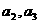 的值及数列
的值及数列 .
.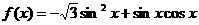 .
. 的值.
的值.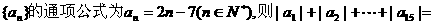 .
.