21.(本小题满分12分)
为防止某突发事件发生,有甲、乙、丙、丁四种相互独立的预防措施可供采用,单独采用甲、乙、丙、丁预防措施后此突发事件不发生的概率(记为P)和所需费用如下表:
|
预防措施 |
甲 |
乙 |
丙 |
丁 |
|
P |
0.9 |
0.8 |
0.7 |
0.6 |
|
费用(万元) |
90 |
60 |
30 |
10 |
预防方案可单独采用一种预防措施或联合采用几种预防措施,在总费用不超过120万元的前提下,请确定一个预防方案,使得此突发事件不发生的概率最大.
20.(本小题满分12分)
直线 的右支交于不同的两点A、B.
的右支交于不同的两点A、B.
(Ⅰ)求实数k的取值范围;
(Ⅱ)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
18.(本小题满分12分)
如图,在棱长为1的正方体ABCD-A1B1C1D1中,AC与BD交于点E,CB与CB1交于点F.
(I)求证:A1C⊥平BDC1;
(II)求二面角B-EF-C的大小(结果用反三角函数值表示).

15.某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n的样本;已知从女学生中抽取的人数为80人,则n= .
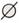 16.设A、B为两个集合,下列四个命题:
16.设A、B为两个集合,下列四个命题:
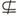
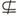 ①A B
①A B 对任意
对任意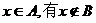 ②A B
②A B


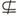
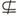 ③A B
③A B A
A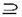 B ④A B
B ④A B 存在
存在
其中真命题的序号是 .(把符合要求的命题序号都填上)
12.设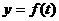 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中 .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
t |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观观察,函数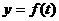 的图象可以近似地看成函数
的图象可以近似地看成函数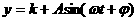 的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
(A)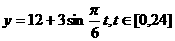 (B)
(B)
(C) (D)
(D)
11.将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子里,每个盒内放一个球,恰好3个球的标号与其在盒子的标号不一致的放入方法种数为
(A)120 (B)240 (C)360 (D)720

 如图,在Rt△ABC中,已知BC=a.若长为2a的线段PQ以点A为中点,问
如图,在Rt△ABC中,已知BC=a.若长为2a的线段PQ以点A为中点,问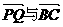 的夹角θ取何值时
的夹角θ取何值时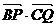 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.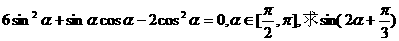 的值.
的值. 的展开式中各项系数的和是128,则展开式中x5的系数是
.(以数字作答)
的展开式中各项系数的和是128,则展开式中x5的系数是
.(以数字作答)