科目:,来源:,题型:
20.(本题12分)已知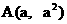 为抛物线
为抛物线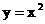 上任意一点, 直线l为过点A的切线, 设直线l交
上任意一点, 直线l为过点A的切线, 设直线l交
y轴于点B. P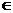 l, 且
l, 且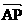
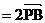 .
.
(1) 当A点运动时, 求点P的轨迹方程;
(2) 求点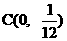 到动直线l的最短距离, 并求此时l的方程.
到动直线l的最短距离, 并求此时l的方程.
点击展开完整题目
试题详情
科目:,来源:,题型:
19. (本题12分) 如图, 四棱锥P-ABCD的底面是正方形, PA⊥底面ABCD, PA=AD=2, 点M、N
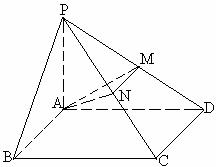 分别为棱PD、PC的中点.
分别为棱PD、PC的中点.
(1) 求证: PD⊥平面AMN;
(2) 求三棱锥P-AMN的体积
(3) 求二面角P-AN-M的大小.
点击展开完整题目
试题详情
科目:,来源:,题型:
18. (本题12分) 已知向量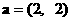 , 向量b与向量a的夹角为
, 向量b与向量a的夹角为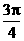 , 且a·b
, 且a·b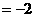 ,
,
(1) 求向量b;
(2) 向量 , 其中A、C是△ABC的内角, 若三角形的三内角A、B、C
, 其中A、C是△ABC的内角, 若三角形的三内角A、B、C
依次成等差数列, 且与x轴垂直. 试求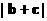 的取值范围.
的取值范围.
点击展开完整题目
试题详情
科目:,来源:,题型:
17.(本题12分)在人寿保险业中, 经过随机抽样统计, 得到某城市投保人能活到80岁的概率
为0.60. 试问:
(1) 3个投保人都能活到80岁的概率;
(2) 3个投保人中只有1人能活到80岁的概率;
(3) 3个投保人至少有1人能活到80岁的概率;
点击展开完整题目
试题详情
科目:,来源:,题型:
16. 有以下四个命题
①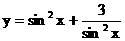 的最小值是
的最小值是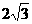
②已知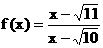 , 则
, 则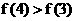
③ 在R上是增函数
在R上是增函数
④函数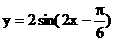 的图象的一个对称点是
的图象的一个对称点是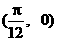
其中真命题的序号是 (把你认为正确命题的序号都填上)
点击展开完整题目
试题详情

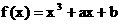 定义在区间
定义在区间 上, 且
上, 且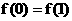 , 设
, 设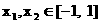
 .
.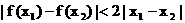
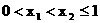 , 求证:
, 求证: 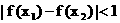 .
.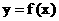 满足条件
满足条件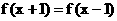 , 且当
, 且当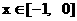 时,
时, ,
,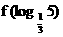 的值是 .
的值是 . , 则
, 则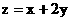 的最大值为
.
的最大值为
.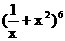 展开式中,
展开式中, 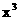 的系数是
. (用数字作答)
的系数是
. (用数字作答)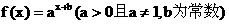 的图象经过点
的图象经过点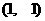 , 且
, 且 , 记
, 记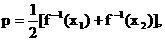
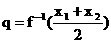 (其中是两个不相等的正实数), 则p与q的大
(其中是两个不相等的正实数), 则p与q的大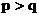 B.
B.
 C.
C.
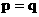 D.
D.