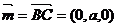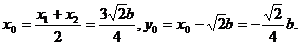1.集合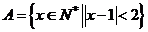 的真子集的个数为
( )
的真子集的个数为
( )
A.3
B.
2.复数(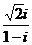 )2(其中i为虚数单位)的虚部等于
( )
)2(其中i为虚数单位)的虚部等于
( )
A.-i B.
3.设函数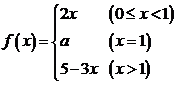 在区间
在区间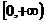 上连续,则实数
上连续,则实数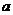 的值为 ( )
的值为 ( )
A.2
B.
4. 已知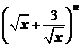 展开式中,各项系数的和与其各项二项式系数的和之比为64,则展开式中的常数项等于
( )
展开式中,各项系数的和与其各项二项式系数的和之比为64,则展开式中的常数项等于
( )
A. 135
B.
5.下面四个命题:
①“直线a∥直线b”的充要条件是“a平行于b所在的平面”;
②“直线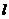 ⊥平面
⊥平面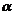 内所有直线”的充要条件是“
内所有直线”的充要条件是“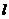 ⊥平面
⊥平面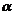 ”;
”;
③“直线a、b为异面直线”的充分不必要条件是“直线a、b不相交”;
④“平面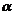 ∥平面
∥平面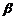 ”的必要不充分条件是“
”的必要不充分条件是“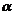 内存在不共线三点到
内存在不共线三点到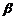 的距离相等”;
的距离相等”;
其中正确命题的序号是 ( )
A.①② B.②③ C.③④ D.②④
6.已知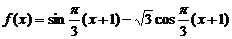 ,则
,则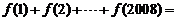 ( )
( )
A.2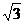 B.
B.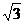 C.1 D.0
C.1 D.0
7.已知O,A,B,C是不共线的四点,若存在一组正实数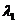 ,
,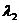 ,
,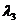 ,使
,使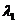
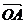 +
+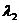
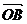 +
+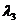
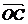 =
= 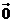 ,则三个角∠AOB,∠BOC,∠COA
( )
,则三个角∠AOB,∠BOC,∠COA
( )
A.都是锐角 B.至多有两个钝角 C.恰有两个钝角 D.至少有两个钝角。
8.由数字0,1,2,3,4,5组成没有重复数字的五位数,所得的数是大于20000的偶数的概率为 ( )
A.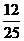 B.
B.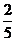 C.
C.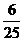 D.
D.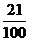
9.双曲线 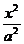 -
-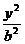 =1的左右焦点分别为F1 ?F2,在双曲线上存在点P,满足?PF1?=5?PF2?。则此双曲线的离心率e的最大值为
( )
=1的左右焦点分别为F1 ?F2,在双曲线上存在点P,满足?PF1?=5?PF2?。则此双曲线的离心率e的最大值为
( )
A.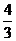 B.
B.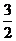 C.
C.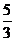 D.2
D.2
10.f (x)是定义在(0,+∞)上的非负可导函数
,且满足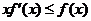 ,对任意的正数
,对任意的正数
a ?b ,若a < b,则必有 ( )
A.a f (a)≤b f (b) B.a f (a)≥b f (b) C.a f (b)≤b f (a) D.a f (b)≥b f (a)
11.已知在平面直角坐标系中,O (0,0), M (1,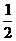 ), N (0,1), Q (2,3), 动点P (x,y)满足:
), N (0,1), Q (2,3), 动点P (x,y)满足:
0≤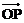
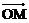 ≤1,0≤
≤1,0≤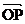
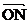 ≤1,则
≤1,则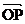
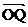 的最大值为_____.
的最大值为_____.
 12.已知函数y=f(x),x∈[-1,1]的图象是由以原点为圆心的两段圆弧及原点构成(如图所示), 则不等式的
12.已知函数y=f(x),x∈[-1,1]的图象是由以原点为圆心的两段圆弧及原点构成(如图所示), 则不等式的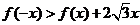 的解集为
的解集为
13.已知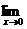
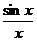 =1,则
=1,则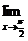
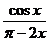 =_____.
=_____.
14.若两条异面直线所成的角为600,则称这对异面直线为“理想异面直线对”,在连接正方体各顶点的所有直线中,“理想异面直线对”的对数为_____.
15.已知抛物线的方程为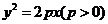 ,直线
,直线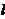 与抛物线交于A,B两点,且以弦AB
与抛物线交于A,B两点,且以弦AB
为直径的圆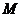 与抛物线的准线相切,则弦AB的中点
与抛物线的准线相切,则弦AB的中点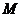 的轨迹方程为
;当直线
的轨迹方程为
;当直线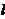 的倾斜角为
的倾斜角为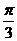 时,圆
时,圆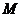 的半径为
.
的半径为
.
16.(本小题满分12分)
已知向量a=(cos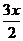 , sin
, sin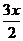 ), b=(cos
), b=(cos ,- sin
,- sin ), 且x∈[0,
), 且x∈[0, 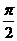 ].
].
(1) 求a・b及?a+b?;
(2)若f (x)= a・b-2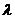 ?a+b?的最小值为-7, 求实数
?a+b?的最小值为-7, 求实数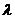 的值.
的值.
17.(本小题满分12分)
某公司科研部研发了甲?乙两种产品的新一代产品,在投产上市前,每种新一代产品都要经过第一和第二两项技术指标检测,两项技术指标的检测结果相互独立,每项技术指标的检测结果都均有A ,B两个等级,对每种新一代产品,当两项技术指标的检测结果均为A级时,才允许投产上市,否则不能投产上市。
(1)已知甲?乙两种新一代产品的每一项技术指标的检测结果为A级的概率如下表所示,分别求出甲?乙两种新一代产品能投产上市的概率P甲?P乙;
第一项技术指标
第二项技术指标
甲
0.8
0.85
乙
0.75
0.8
(2)若甲?乙两种新一代产品能投产上市,可分别给公司创造100万元?150万元的利润;否则将分别给公司造成10万元?20万元的损失,在1)的条件下,用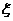 ?
?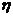 分别表示甲?乙两种新一代产品的研发给公司创造的利润,求
分别表示甲?乙两种新一代产品的研发给公司创造的利润,求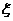 ?
?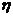 的分布列及E
的分布列及E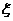 ?E
?E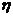 .
.
18.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B = 900,D为棱BB1上一点,且面DA1 C⊥面AA1C1C.
1)求证:D点为棱BB1的中点;
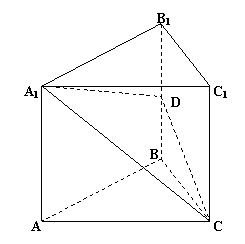 2)若二面角A -A1D - C的平面角为600,求
2)若二面角A -A1D - C的平面角为600,求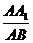 的值。
的值。
19.(本小题满分13分)设正项数列{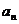 }的前项和为Sn,q为非零常数。已知对任意正整数n, m,当n > m时,
}的前项和为Sn,q为非零常数。已知对任意正整数n, m,当n > m时,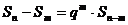 总成立。
总成立。
1)求证数列{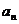 }是等比数列;
}是等比数列;
2)若正整数n, m, k成等差数列,求证: 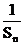 +
+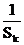 ≥
≥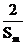 。
。
20.(本小题满分13分)已知椭圆C: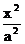 +
+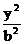 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为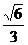 ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
1)求直线ON(O为坐标原点)的斜率KON ;
2)对于椭圆C上任意一点M ,试证:总存在角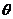 (
(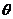 ∈R)使等式:
∈R)使等式:
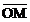 =cos
=cos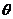
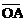 +sin
+sin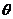
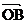 成立。
成立。
21.(本小题满分13分)
我们知道:函数y=f (x)如果存在反函数y=f -1 (x),则y=f (x)的图像与y=f -1 (x)图像关于直线y=x对称。若y=f (x)的图像与y=f -1 (x)的图像有公共点,其公共点却不一定都在直线y=x上;例如函数f (x)=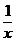 。
。
(1)若函数y=f (x)在其定义域上是增函数,且y=f (x)的图像与其反函数y=f -1 (x)的图像有公共点,证明这些公共点都在直线y=x上;
(2)对问题:“函数f (x)=a x (a>1)与其反函数f -1 (x)=logax的图像有多少个公共点?”有如下观点:
观点①:“当a>1时两函数图像没有公共点,只有当0<a<1时两函数图像才有公共点”。
观点②:“利用(1)中的结论,可先讨论函数f (x)=a x (a>1)的图像与直线y=x的公共点的个数,为此可构造函数F (x)=a x-x(a>1),然后可利用F (x)的最小值进行讨论”。
请参考上述观点,讨论函数f (x)=ax (a>1)与其反函数f -1 (x)=logax图像公共点的个数。
数学试卷(理科)参考解答
题序
1
2
3
4
5
6
7
8
9
10
答案
A
C
A
C
D
B
D
B
B
C
11. 4. 12. [-1,-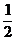 )∪(0,
)∪(0, 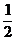 ).. 13.
).. 13. 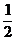 。 14. 24.
。 14. 24.
15. 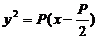 (3分)、
(3分)、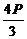 (2分)。
(2分)。
16.解:(1)∵ a = (cos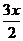 , sin
, sin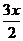 ), b = (cos
), b = (cos ,- sin
,- sin )
)
∴ a・b =cos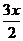 cos
cos +sin
+sin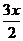 (- sin
(- sin )=cos
)=cos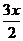 cos
cos -sin
-sin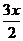 sin
sin
=cos(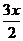 +
+ )=cos2x
………3分
)=cos2x
………3分
又易知:?a?=1,?b?=1 ∴?a+b?2 = a 2+b 2+2 a・b
=1+1+2 cos2x=4cos2x ,且x∈[0, 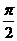 ],
],
∴?a+b?=2cosx. ………6分
(2) f (x)= a・b-2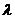 ?a+b?
?a+b?
=cos2x-2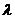 (2cosx)
(2cosx)
=2cos2x-4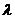 cosx - 1
cosx - 1
=2(cosx-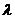 )2-2
)2-2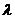 2-1
………8分
2-1
………8分
若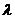 <0,当cosx=0时,f (x)取得最小值-1,不合题意;
<0,当cosx=0时,f (x)取得最小值-1,不合题意;
若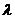 >1,当cosx=1时,f (x)取得最小值1-4
>1,当cosx=1时,f (x)取得最小值1-4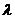 ,由题意有1-4
,由题意有1-4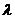 =-7,得
=-7,得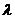 =2;
=2;
若0≤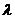 ≤1,当cosx=
≤1,当cosx=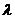 时,f (x)取得最小值-2
时,f (x)取得最小值-2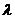 2-1,由题意有-2
2-1,由题意有-2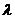 2-1=-7,得
2-1=-7,得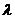 =±
=±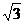 (舍去)。
(舍去)。
综上所述: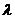 =2。
………12分
=2。
………12分
17.解: 1)由题意有: P甲 = 0.8×0.85= 0.68 ; ………3分
P乙 = 0.75×0.8= 0.6 。 ………6分
2)随机变量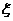 ?
?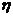 的分布列分别是:
的分布列分别是:
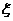
100
-10
P
0.68
0.32
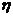
150
-20
P
0.6
0.4
………9分
E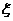 = 100×0.68+(-10)×0.32 = 64.8 ;
= 100×0.68+(-10)×0.32 = 64.8 ;
E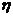 = 150×0.6+(-20)×0.4 = 82 。
………12分
= 150×0.6+(-20)×0.4 = 82 。
………12分
18.解: 1)过点D作DE ⊥ A1 C 于E点,取AC的中点F,连BF ?EF。
∵面DA1 C⊥面AA1C1C且相交于A1 C,面DA1 C内的直线DE ⊥ A1 C
∴直线DE⊥面AA1C1C ………3分
又∵面BA C⊥面AA1C1C且相交于AC,易知BF⊥AC,
∴BF⊥面AA1C1C
由此知:DE∥BF ,从而有D,E,F,B共面,
又易知BB1∥面AA1C1C,故有DB∥EF ,从而有EF∥AA1,
又点F是AC的中点,所以DB = EF = 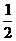 AA1 =
AA1 = 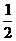 BB1,
BB1,
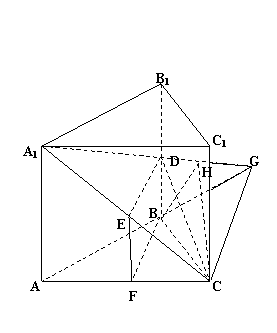 所以D点为棱BB1的中点;
………6分
所以D点为棱BB1的中点;
………6分
2)解法1:延长A1 D与直线AB相交于G,易知CB⊥面AA1B1B,
过B作BH⊥A1 G于点H,连CH,由三垂线定理知:A1 G⊥CH,
由此知∠CHB为二面角A -A1D - C的平面角; ………9分
设AA1 = 2b ,AB=BC =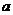 ;
;
在直角三角形A1A G中,易知 AB = BG。
在直角三角形DB G中,BH = 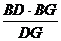 =
= 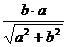 ,
,
在直角三角形CHB中,tan∠CHB = 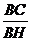 =
=  ,
,
据题意有: = tan600 =
= tan600 = 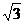 ,解得:
,解得: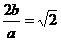 ,
,
所以 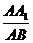 =
=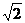 。
………12分
。
………12分
2)解法2:建立如图所示的直角坐标系,设AA1 =
2b ,AB=BC =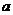 ,
,
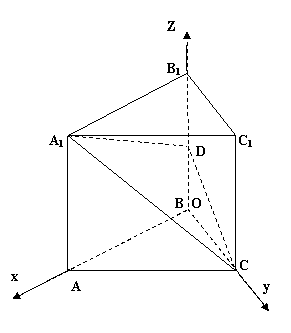 则D(0,0,b), A1 (a,0,2b), C (0,a,0)
则D(0,0,b), A1 (a,0,2b), C (0,a,0)
所以,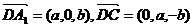 ………8分
………8分
设面DA1C的法向量为
则 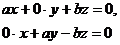
可取
又可取平面AA1DB的法向量
cos〈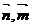 〉
〉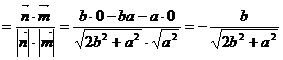 ………10分
………10分
据题意有: ,解得:
,解得: 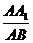 =
=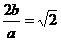 ………12分
………12分
说明:考生的其他不同解法,请参照给分。
19.解: 1)因为对任意正整数n, m,当n > m时,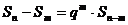 总成立。
总成立。
所以当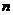 ≥2时:
≥2时: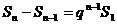 ,即
,即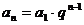 ,且
,且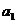 也适合,又
也适合,又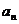 >0,
>0,
故当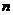 ≥2时:
≥2时: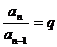 (非零常数),即{
(非零常数),即{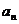 }是等比数列。
………5分
}是等比数列。
………5分
2)若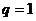 ,则
,则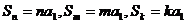 。所以
。所以
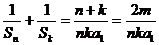 ≥
≥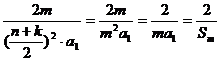 。
………7分
。
………7分
若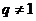 ,则
,则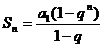 ,
,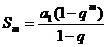 ,
, 。 ………8分
。 ………8分
所以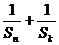 ≥
≥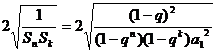 。
………10分
。
………10分
又因为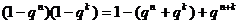
≤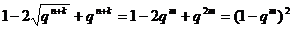 。所以
。所以
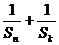 ≥
≥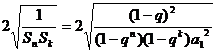 ≥
≥ 。
。
综上可知:若正整数n, m,
k成等差数列,不等式
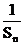 +
+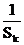 ≥
≥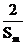 总成立。
总成立。
当且仅当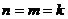 时取“=”。
………13分
时取“=”。
………13分
20.解: 1)设椭圆的焦距为2c,因为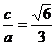 ,所以有
,所以有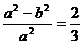 ,故有
,故有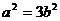 。从而椭圆C的方程可化为:
。从而椭圆C的方程可化为: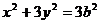 ①
………2分
①
………2分
易知右焦点F的坐标为(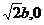 ),
),
据题意有AB所在的直线方程为: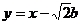 ②
………3分
②
………3分
由①,②有: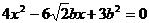 ③
③
设 ,弦AB的中点
,弦AB的中点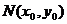 ,由③及韦达定理有:
,由③及韦达定理有:
所以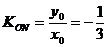 ,即为所求。
………5分
,即为所求。
………5分
2)显然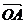 与
与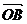 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量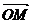 ,有且只有一对实数
,有且只有一对实数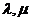 ,使得等式
,使得等式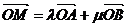 成立。设
成立。设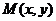 ,由1)中各点的坐标有:
,由1)中各点的坐标有:
 ,所以
,所以
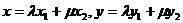 。
………7分
。
………7分
又点在椭圆C上,所以有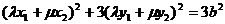 整理为
整理为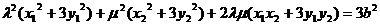 。
④
。
④
由③有: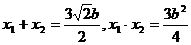 。所以
。所以
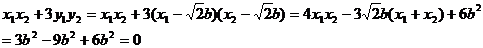 ⑤
⑤
又A?B在椭圆上,故有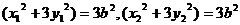 ⑥
⑥
将⑤,⑥代入④可得: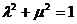 。
………11分
。
………11分
对于椭圆上的每一个点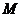 ,总存在一对实数,使等式
,总存在一对实数,使等式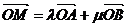 成立,而
成立,而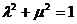
在直角坐标系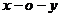 中,取点P(
中,取点P(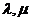 ),设以x轴正半轴为始边,以射线OP为终边的角为
),设以x轴正半轴为始边,以射线OP为终边的角为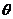 ,显然
,显然 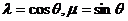 。
。
也就是:对于椭圆C上任意一点M ,总存在角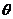 (
(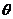 ∈R)使等式:
∈R)使等式: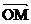 =cos
=cos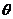
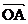 +sin
+sin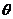
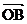 成立。
………13分
成立。
………13分
21.解; 1)设点M(x0, y0)是函数y = f (x)的图像与其反函数y = f -1 (x)的图像的公
点,则有:y0=f (x0) ,
y0 = f -1 (x0),据反函数的意义有:x0 = f (y0)。 ………2分
所以:y0 = f (x0)且同时有x0 = f (y0)。
若x0 < y0 ,因为函数y = f (x) 是其定义域上是增函数,
所以有:f (x0) < f (y0) ,即y0 < x0 与 x0 < y0矛盾,这说明x0 < y0是错误的。
同理可证x0 > y0也是错误的。
所以x0 = y0 ,即函数y = f (x)的图像与其反函数y = f -1 (x)的图像有公共点在直线y = x上; ………5分
2)构造函数F (x)=a x-x(a>1)
因为F′ (x)= a xlna - 1(a > 1), ………6分
令F′ (x)= a xlna - 1≥0,
解得:x ≥ 。
。
所以当x ≥ 时:F′ (x)≥0,F (x)在区间
时:F′ (x)≥0,F (x)在区间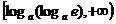 上是增函数;
上是增函数;
当x
≤ 时:F′ (x)≤0,F (x)在区间
时:F′ (x)≤0,F (x)在区间 上是减函数。
上是减函数。
所以F (x)的最小值为F (x)min=F ( )=
)=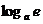 -
- 。………9分
。………9分
令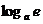 -
- >0,解得:a >
>0,解得:a >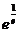 。
。
故当a>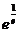 时:F (x)min =F (
时:F (x)min =F ( )>0,所以方程F (x)=a x-x
=0无实数解,这说明函数f (x)=a x (a>1)的图像与直线y=x没有公共点;
………10分
)>0,所以方程F (x)=a x-x
=0无实数解,这说明函数f (x)=a x (a>1)的图像与直线y=x没有公共点;
………10分
当a=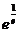 时:F (x)min =F (
时:F (x)min =F ( )=F (e)=0,所以方程F (x)=a x-x
=0有唯一实数解x =
)=F (e)=0,所以方程F (x)=a x-x
=0有唯一实数解x = =e。这说明函数f (x)=a x (a>1)的图像与直线y=x有唯一公共点;
………11分
=e。这说明函数f (x)=a x (a>1)的图像与直线y=x有唯一公共点;
………11分
当a<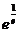 时:F (x)min =F (
时:F (x)min =F ( )<0,所以方程F (x)=a x-x
=0有两相异的实数解
)<0,所以方程F (x)=a x-x
=0有两相异的实数解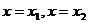 (设
(设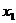 <
<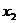 )。
)。
又因为当x → -∞或x → +∞时有F (x) → +∞,且F (0)=1,所以据函数
F (x)=a x-x(a>1)的单调性可知:-∞<0<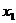 <
< <
<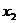 <+∞,这说明函数f (x)=a x (a>1)的图像与直线y=x有两不同的公共点个公共点。 ………12分
<+∞,这说明函数f (x)=a x (a>1)的图像与直线y=x有两不同的公共点个公共点。 ………12分
综上所述:
当a>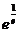 时: 函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像没有公共点;
时: 函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像没有公共点;
当a =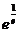 时:函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像有唯一公共点;
时:函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像有唯一公共点;
当1<a<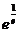 时:函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像有两个不同的公共点。
………13分
时:函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像有两个不同的公共点。
………13分