【题目】已知函数f(x)为对数函数,并且它的图象经过点(2 ![]() ,
, ![]() ),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
(1)求函数f(x)的解析式;
(2)求函数y=g(x)在区间[ ![]() ,16]上的最小值.
,16]上的最小值.
参考答案:
【答案】
(1)解:设f(x)=logax(a>0且a≠1)
∵f(x)的图象经过点 ![]() ,∴
,∴ ![]() ,即
,即 ![]()
∴ ![]() ,即a=2
,即a=2
∴f(x)=log2x(x>0)
(2)解:设t=f(x)=log2x,∵ ![]() ,∴
,∴ ![]()
∴ ![]() ,即
,即 ![]()
则y=g(t)=t2﹣2bt+3=(t﹣b)2+3﹣b2, ![]() ,对称轴为t=b
,对称轴为t=b
①当 ![]() 时,y=g(t)在
时,y=g(t)在 ![]() 上是增函数,
上是增函数, ![]()
②当 ![]() 时,y=g(t)在
时,y=g(t)在 ![]() 上是减函数,在(b,4]上是增函数,
上是减函数,在(b,4]上是增函数, ![]()
③当b>4时,y=g(t)在 ![]() 上是减函数,ymin=g(4)=19﹣8b
上是减函数,ymin=g(4)=19﹣8b
综上所述, 
【解析】(1)设f(x)=logax(a>0且a≠1,代值计算即可求出函数的解析式,(2)设t=f(x)=log2x则y=g(t)=(t﹣b)2+3﹣b2 , 对称轴为t=b,再利用对称轴与区间的位置关系,进行分类讨论,从而可求函数y=g(x)在区间[ ![]() ,16]上的最小值
,16]上的最小值
【考点精析】通过灵活运用函数的最值及其几何意义,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的奇函数,当x≤0时,f(x)=x(2+x).
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图象,并写出单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次订购多少件服装时,该服装厂获得的利润最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
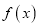 在
在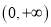 存在最小值,求
存在最小值,求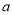 的取值范围;
的取值范围;(Ⅱ)当
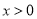 时,证明:
时,证明: 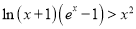 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数f(x)=
 是奇函数.
是奇函数.
(1)求b的值;
(2)判断函数f(x)在R上的单调性并加以证明;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
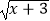 +
+ 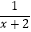 的定义域为( )
的定义域为( )
A.{x|x≥﹣3且x≠﹣2}
B.{x|x≥﹣3且x≠2}
C.{x|x≥﹣3}
D.{x|x≥﹣2且x≠3} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数F(x)=g(x)+h(x)=ex , 且g(x),h(x)分别是R上的偶函数和奇函数,若对任意的x∈(0,+∞),不等式g(2x)≥ah(x)恒成立,则实数a的取值范围是( )
A.(﹣∞,2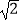 ]
]
B.(﹣∞,2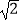 )
)
C.(﹣∞,2]
D.(﹣∞,2)
相关试题

