【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求b的值;
(2)判断函数f(x)在R上的单调性并加以证明;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
参考答案:
【答案】
(1)解∵函数为定义在R上的奇函数,
∴f(0)=0,
∴ ![]() =0
=0
解得b=1
(2)解由(1)知f(x)= ![]() =
= ![]() =
= ![]() +
+ ![]() ,
,
设x1,x2∈R,且x1<x2,
则f(x1)﹣f(x2)= ![]() +
+ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() >0,
>0,
∴函数f(x)为减函数
(3)解∵f(t2﹣2t)+f(2t2﹣k)<0,
∴f(t2﹣2t)<﹣f(2t2﹣k)=f(﹣2t2+k)恒成立,
∵函数f(x)在R上为减函数.
∴t2﹣2t>﹣2t2+k,
∴k<3t2﹣2t=3(t﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴k<﹣ ![]() ,
,
故k的取值范围为(﹣∞, ![]() )
)
【解析】(1)根据奇函数的性质推断出f(0)=0求得b的值.(2)先分离常数,再利用单调性的定义证明即可.(3)根据奇函数的性质和函数的单调性,得到t2﹣2t>﹣2t2+k,再分离参数k,求出函数3t2﹣2t的最小值即可.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次订购多少件服装时,该服装厂获得的利润最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
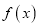 在
在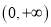 存在最小值,求
存在最小值,求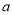 的取值范围;
的取值范围;(Ⅱ)当
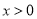 时,证明:
时,证明: 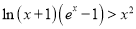 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)为对数函数,并且它的图象经过点(2
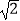 ,
,  ),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
(1)求函数f(x)的解析式;
(2)求函数y=g(x)在区间[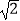 ,16]上的最小值.
,16]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
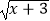 +
+ 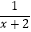 的定义域为( )
的定义域为( )
A.{x|x≥﹣3且x≠﹣2}
B.{x|x≥﹣3且x≠2}
C.{x|x≥﹣3}
D.{x|x≥﹣2且x≠3} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数F(x)=g(x)+h(x)=ex , 且g(x),h(x)分别是R上的偶函数和奇函数,若对任意的x∈(0,+∞),不等式g(2x)≥ah(x)恒成立,则实数a的取值范围是( )
A.(﹣∞,2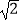 ]
]
B.(﹣∞,2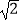 )
)
C.(﹣∞,2]
D.(﹣∞,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N* , 有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn= ,求数列{bn}的前n项和T.
,求数列{bn}的前n项和T.
相关试题

