【题目】已知函数![]() .
.
(Ⅰ)若![]() 在
在![]() 存在最小值,求
存在最小值,求![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,证明:
时,证明: ![]() .
.
参考答案:
【答案】(1)![]() 在
在![]() 上无最小值.(2)见解析
上无最小值.(2)见解析
【解析】试题分析:(Ⅰ)对函数![]() 求导,分情况讨论单调性,当
求导,分情况讨论单调性,当![]() 有最小值时,求出实数
有最小值时,求出实数![]() 的范围;(Ⅱ)本题分两部分证明,先证明
的范围;(Ⅱ)本题分两部分证明,先证明![]() ,由(Ⅰ)的讨论容易得到,再证明
,由(Ⅰ)的讨论容易得到,再证明![]() ,这是构造函数
,这是构造函数![]() ,求导得出函数
,求导得出函数![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,就可证明
,就可证明![]() ,结合
,结合![]() 和
和![]() ,便可得出结论.
,便可得出结论.
试题解析(Ⅰ)解: 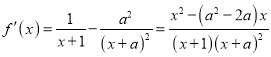
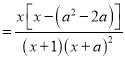 ,
,
令![]() ,解得:
,解得: ![]() 或
或![]() .
.
(1)当![]() 时,即
时,即![]() ,由
,由![]() 知,
知, ![]() ,
,
故![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() 在
在![]() 上无最小值.
上无最小值.
(2)当![]() 时,又
时,又![]() ,故
,故![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
从而![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
从而![]() 在
在![]() 处取得最小值,所以
处取得最小值,所以![]() 时,
时, ![]() 存在最小值.
存在最小值.
综上所述: ![]() 在
在![]() 存在最小值时,
存在最小值时, ![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)证明:由(Ⅰ)知, ![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
于是![]() 时,
时, ![]() ,即
,即![]() 时,
时, ![]() .①
.①
下证: ![]() ,
,
令![]() ,则
,则![]() ,故
,故![]() ,
,
由于![]() ,所以
,所以![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
于是![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
故![]() ,所以
,所以![]() ,②
,②
由于![]() ,所以①②可得:
,所以①②可得: ![]() ,
,
即: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆
 和直线
和直线 .
.(Ⅰ)求
 的参数方程以及圆
的参数方程以及圆 上距离直线
上距离直线 最远的点
最远的点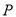 坐标;
坐标;(Ⅱ)以坐标原点
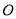 为极点,
为极点,  轴正半轴为极轴建立极坐标系,将圆
轴正半轴为极轴建立极坐标系,将圆 上除点
上除点 以外所有点绕着
以外所有点绕着 逆时针旋转
逆时针旋转 得到曲线
得到曲线 ,求曲线
,求曲线 的极坐标方程.
的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的奇函数,当x≤0时,f(x)=x(2+x).
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图象,并写出单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次订购多少件服装时,该服装厂获得的利润最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)为对数函数,并且它的图象经过点(2
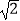 ,
,  ),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
(1)求函数f(x)的解析式;
(2)求函数y=g(x)在区间[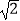 ,16]上的最小值.
,16]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数f(x)=
 是奇函数.
是奇函数.
(1)求b的值;
(2)判断函数f(x)在R上的单调性并加以证明;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
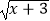 +
+ 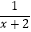 的定义域为( )
的定义域为( )
A.{x|x≥﹣3且x≠﹣2}
B.{x|x≥﹣3且x≠2}
C.{x|x≥﹣3}
D.{x|x≥﹣2且x≠3}
相关试题

