【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)求![]() 在
在![]() 上的单调区间;
上的单调区间;
(Ⅱ)求![]() 在
在![]() (
(![]() 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
参考答案:
【答案】(1)单调减区间为![]() ,
,![]() :单调增区间为
:单调增区间为![]()
(2) 当![]() 时,最大值为
时,最大值为![]() ;当
;当![]() 时,最大值为2.
时,最大值为2.
【解析】试题分析:(1)当x<1时,利用导数可求得![]() ,所以所以
,所以所以![]() 在
在![]() 上的单调减区间为
上的单调减区间为![]() ,
,![]() :单调增区间为
:单调增区间为![]() .(2) 分段函数分段做,先处理当
.(2) 分段函数分段做,先处理当![]() 时, 由(Ⅰ)知在
时, 由(Ⅰ)知在![]()
![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增,从而
上单调递增,从而![]() 在
在![]() 处取得极大值
处取得极大值![]() ,最大值f(-1)=2,当
,最大值f(-1)=2,当![]() 时,
时,![]() ,(
,(![]() ),
),![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上的最大值为
上的最大值为![]() .两个区间上的最大值a与2进行比较,所以当
.两个区间上的最大值a与2进行比较,所以当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() ;当
;当![]() 时,
时,![]() 在
在![]() 上的最大值为2.
上的最大值为2.
试题解析:(Ⅰ)因为![]()
当![]() 时,
时,![]() ,
,
解![]() 得到
得到![]() ;解
;解![]() 得到
得到![]() 或
或![]() .所以
.所以![]() 在
在![]() 上的单调减区间为
上的单调减区间为![]() ,
,![]() :单调增区间为
:单调增区间为![]()
(Ⅱ)①当![]() 时,由(Ⅰ)知在
时,由(Ⅰ)知在![]()
![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增,从而
上单调递增,从而![]() 在
在![]() 处取得极大值
处取得极大值![]() .
.
又![]() ,所以
,所以![]() 在
在![]() 上的最大值为2.
上的最大值为2.
②当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上的最大值为
上的最大值为![]() .所以当
.所以当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() ;当
;当![]() 时,
时,![]() 在
在![]() 上的最大值为2.
上的最大值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),且对任意的x1∈[﹣1,2],都存在x2∈[﹣1,2],使f(x2)=g(x1),则实数a的取值范围是( )
A.[3,+∞)
B.(0,3]
C.[ ,3]
,3]
D.(0, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
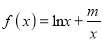 ,m∈R.
,m∈R.(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数
 零点的个数.
零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】☉O为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE为☉O的切线,求△ADE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=x2﹣ax+b,其图象对称轴为直线x=2,且g(x)的最小值为﹣1,设f(x)=
 .
.
(1)求实数a,b的值;
(2)若不等式f(3x)﹣t3x≥0在x∈[﹣2,2]上恒成立,求实数t的取值范围;
(3)若关于x的方程f(|2x﹣2|)+k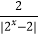 ﹣3k=0有三个不同的实数解,求实数k的取值范围.
﹣3k=0有三个不同的实数解,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,若
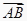 =a,
=a,  =b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
=b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
A.平行四边形
B.矩形
C.菱形
D.正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x>1},B={x|x≥2}.
(1)求集合A∩(RB);
(2)若集合C={x|x﹣a>0},且满足A∩C=C,求实数a的取值范围.
相关试题

