【题目】设函数![]() ,m∈R.
,m∈R.
(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数![]() 零点的个数.
零点的个数.
参考答案:
【答案】(1)当x=e时,f(x)取得极小值2(2)见解析
【解析】试题分析:(1)求函数的导数![]() ,函数的极值点为
,函数的极值点为![]() ,所以得到函数的单调区间,也就得到函数的最小值了;(2)根据
,所以得到函数的单调区间,也就得到函数的最小值了;(2)根据![]() ,参变分离后得到
,参变分离后得到![]() ,设
,设![]() ,通过导数求函数的单调性,以及图象特征,转化为
,通过导数求函数的单调性,以及图象特征,转化为![]() 与函数的交点个数问题.
与函数的交点个数问题.
试题解析:(1)当![]() 时,
时, ![]() ,∴
,∴![]()
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函;
上是增函;
∴当![]() 时,
时, ![]() 取最小值
取最小值![]() .
.
(2)∵函数![]() ,
,
令![]() ,得
,得![]() ;
;
设![]() ,则
,则![]()
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 是
是![]() 的极值点,且是唯一极大值点,∴
的极值点,且是唯一极大值点,∴![]() 是
是![]() 的最大值点;
的最大值点;
∴![]() 的最大值为
的最大值为![]() ,又
,又![]() 结合
结合![]() 的图像,
的图像,
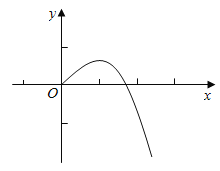
可知:
①当![]() 时,函数
时,函数![]() 无零点;
无零点;
②当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
③当![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
④当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
综上:
当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点;当
有且只有一个零点;当![]() 时,函数
时,函数![]() 有且只有两个零点.
有且只有两个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.y=x
B.y=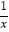
C.y=﹣x3
D.y=( )x
)x -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=loga(2﹣ax)是[0,1]上的减函数,则a的取值范围为 ( )
A. (0,1) B. (1,2) C. (0,2) D. (2,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),且对任意的x1∈[﹣1,2],都存在x2∈[﹣1,2],使f(x2)=g(x1),则实数a的取值范围是( )
A.[3,+∞)
B.(0,3]
C.[ ,3]
,3]
D.(0, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】☉O为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE为☉O的切线,求△ADE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
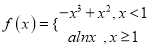 ,其中
,其中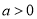 .
.(Ⅰ)求
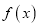 在
在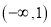 上的单调区间;
上的单调区间;(Ⅱ)求
 在
在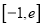 (
(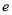 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=x2﹣ax+b,其图象对称轴为直线x=2,且g(x)的最小值为﹣1,设f(x)=
 .
.
(1)求实数a,b的值;
(2)若不等式f(3x)﹣t3x≥0在x∈[﹣2,2]上恒成立,求实数t的取值范围;
(3)若关于x的方程f(|2x﹣2|)+k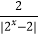 ﹣3k=0有三个不同的实数解,求实数k的取值范围.
﹣3k=0有三个不同的实数解,求实数k的取值范围.
相关试题

