【题目】在四边形ABCD中,若 ![]() =a,
=a, ![]() =b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
=b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
A.平行四边形
B.矩形
C.菱形
D.正方形
参考答案:
【答案】B
【解析】解答:以 ![]() 为邻边作平行四边形,依据向量加法的平行四边形法则和向量减法的三角形法则可得a+b,a-b分别对应两条对角线.因为|a+b|=|a-b|,所以两条对角线相等,所以四边形ABCD是矩形.
为邻边作平行四边形,依据向量加法的平行四边形法则和向量减法的三角形法则可得a+b,a-b分别对应两条对角线.因为|a+b|=|a-b|,所以两条对角线相等,所以四边形ABCD是矩形.
分析:本题主要考查了向量的三角形法则、向量加减混合运算及其几何意义,解决问题的关键是根据向量的运算性质结合所给四边形满足的条件分析判断即可.
【考点精析】掌握向量的三角形法则是解答本题的根本,需要知道三角形加法法则的特点:首尾相连;三角形减法法则的特点:共起点,连终点,方向指向被减向量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】☉O为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE为☉O的切线,求△ADE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
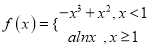 ,其中
,其中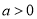 .
.(Ⅰ)求
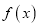 在
在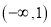 上的单调区间;
上的单调区间;(Ⅱ)求
 在
在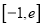 (
(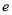 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=x2﹣ax+b,其图象对称轴为直线x=2,且g(x)的最小值为﹣1,设f(x)=
 .
.
(1)求实数a,b的值;
(2)若不等式f(3x)﹣t3x≥0在x∈[﹣2,2]上恒成立,求实数t的取值范围;
(3)若关于x的方程f(|2x﹣2|)+k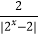 ﹣3k=0有三个不同的实数解,求实数k的取值范围.
﹣3k=0有三个不同的实数解,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x>1},B={x|x≥2}.
(1)求集合A∩(RB);
(2)若集合C={x|x﹣a>0},且满足A∩C=C,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
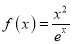 ,
, 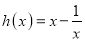 .
.(I)求函数
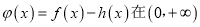 上零点的个数;
上零点的个数; (II)设
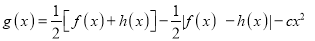 ,若函数
,若函数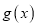 在
在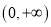 上是增函数.
上是增函数.求实数
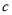 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某辆汽车以x km/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为
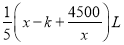 ,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.
,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.(1)求k的值;
(2)求该汽车每小时油耗的最小值.
相关试题

