【题目】☉O为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE为☉O的切线,求△ADE的周长.
参考答案:
【答案】解:如图,设☉O与△ABC各边的切点分别为F,G,H,则 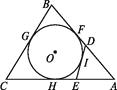
AF=AH,BF=BG,CG=CH,且AF+BF=9,BG+CG=8,CH+AH=10,
∴AF=AH=5.5,BF=BG=3.5,CG=CH=4.5.
又DE是☉O的切线,∴DI=DF,EI=EH.
∴△ADE的周长=AD+DE+EA=AD+DI+EI+EA=AF+AH=2AF=2×5.5=11.
【解析】本题主要考查了与圆有关的比例线段,解决问题的关键是根据与圆有关的比例线段满足的切线定理结合三角形的有关性质分析计算即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=loga(2﹣ax)是[0,1]上的减函数,则a的取值范围为 ( )
A. (0,1) B. (1,2) C. (0,2) D. (2,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),且对任意的x1∈[﹣1,2],都存在x2∈[﹣1,2],使f(x2)=g(x1),则实数a的取值范围是( )
A.[3,+∞)
B.(0,3]
C.[ ,3]
,3]
D.(0, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
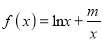 ,m∈R.
,m∈R.(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数
 零点的个数.
零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
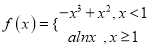 ,其中
,其中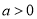 .
.(Ⅰ)求
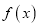 在
在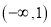 上的单调区间;
上的单调区间;(Ⅱ)求
 在
在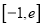 (
(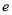 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=x2﹣ax+b,其图象对称轴为直线x=2,且g(x)的最小值为﹣1,设f(x)=
 .
.
(1)求实数a,b的值;
(2)若不等式f(3x)﹣t3x≥0在x∈[﹣2,2]上恒成立,求实数t的取值范围;
(3)若关于x的方程f(|2x﹣2|)+k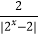 ﹣3k=0有三个不同的实数解,求实数k的取值范围.
﹣3k=0有三个不同的实数解,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,若
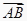 =a,
=a,  =b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
=b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
A.平行四边形
B.矩形
C.菱形
D.正方形
相关试题

