【题目】设集合A={x|x>1},B={x|x≥2}.
(1)求集合A∩(RB);
(2)若集合C={x|x﹣a>0},且满足A∩C=C,求实数a的取值范围.
参考答案:
【答案】
(1)解:由题意得,B={x|x≥2},
则RB={x|x<2},
又A={x|x>1},所以A∩(RB)={x|1<x<2}
(2)解:C={x|x﹣a>0}={x|x>a},
由A∩C=C得,CA,
所以a≥1,即实数a的取值范围是[1,+∞)
【解析】(1)由题意和补集的运算求出RB,由交集的运算求出A∩(RB);(2)先求出集合C,由A∩C=C得CA,根据子集的定义求出实数a的取值范围.
【考点精析】根据题目的已知条件,利用集合的交集运算和交、并、补集的混合运算的相关知识可以得到问题的答案,需要掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立;求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.
B,反之也成立;求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
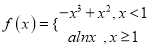 ,其中
,其中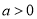 .
.(Ⅰ)求
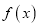 在
在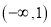 上的单调区间;
上的单调区间;(Ⅱ)求
 在
在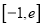 (
(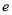 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=x2﹣ax+b,其图象对称轴为直线x=2,且g(x)的最小值为﹣1,设f(x)=
 .
.
(1)求实数a,b的值;
(2)若不等式f(3x)﹣t3x≥0在x∈[﹣2,2]上恒成立,求实数t的取值范围;
(3)若关于x的方程f(|2x﹣2|)+k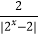 ﹣3k=0有三个不同的实数解,求实数k的取值范围.
﹣3k=0有三个不同的实数解,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,若
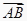 =a,
=a,  =b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
=b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
A.平行四边形
B.矩形
C.菱形
D.正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
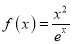 ,
, 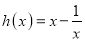 .
.(I)求函数
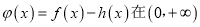 上零点的个数;
上零点的个数; (II)设
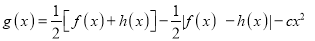 ,若函数
,若函数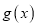 在
在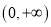 上是增函数.
上是增函数.求实数
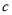 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某辆汽车以x km/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为
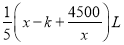 ,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.
,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.(1)求k的值;
(2)求该汽车每小时油耗的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信已成为人们常用的社交软件,“微信运动”是微信里由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的
 或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:步数
性别
0
 2000
20002001
 5000
50005001
 8000
80008001
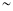 10000
10000>10000
男
1
2
4
7
6
女
0
3
9
6
2
若某人一天的走路步数超过8000步被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)利用样本估计总体的思想,试估计小明的所有微信好友中每日走路步数超过10000步的概率;
(2)根据题意完成下面的
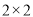 列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?积极型
懈怠型
总计
男
女
总计
附:
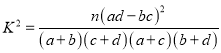
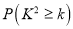
0.10
0.05
0.010
0.005
0.001
2.706
3.841
6.635
7.879
10.828
相关试题

