【题目】已知函数g(x)=x2﹣ax+b,其图象对称轴为直线x=2,且g(x)的最小值为﹣1,设f(x)= ![]() .
.
(1)求实数a,b的值;
(2)若不等式f(3x)﹣t3x≥0在x∈[﹣2,2]上恒成立,求实数t的取值范围;
(3)若关于x的方程f(|2x﹣2|)+k ![]() ﹣3k=0有三个不同的实数解,求实数k的取值范围.
﹣3k=0有三个不同的实数解,求实数k的取值范围.
参考答案:
【答案】
(1)解:∵函数g(x)=x2﹣ax+b,其图象对称轴为直线x=2,
∴ ![]() =2,
=2,
解得:a=4,
当x=2时,函数取最小值b﹣4=﹣1,
解得:b=3
(2)解:由(1)得:g(x)=x2﹣4x+3,
f(x)=x﹣4+ ![]()
若不等式f(3x)﹣t3x≥0在x∈[﹣2,2]上恒成立,
则t≤ ![]() 在x∈[﹣2,2]上恒成立,
在x∈[﹣2,2]上恒成立,
当3x= ![]() ,即x=log32﹣1时,
,即x=log32﹣1时, ![]() 取最小值﹣
取最小值﹣ ![]() ,
,
故t≤﹣ ![]()
(3)解:令t=|2x﹣2|,t≥0,
则原方程可化为:t+ ![]() ﹣4+
﹣4+ ![]() ﹣3k=0,
﹣3k=0,
即t2﹣(4+3k)t+(3+2k)=0,
若关于x的方程f(|2x﹣2|)+k ![]() ﹣3k=0有三个不同的实数解,
﹣3k=0有三个不同的实数解,
则方程t2﹣(4+3k)t+(3+2k)=0有两个根,
其中一个在区间(0,2)上,一个在区间[2,+∞),
令h(t)=t2﹣(4+3k)t+(3+2k),
则 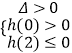 ,
,
即 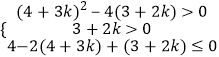 ,
,
解得:k∈[﹣ ![]() ,+∞)
,+∞)
【解析】(1)根据函数g(x)=x2﹣ax+b,其图象对称轴为直线x=2,且g(x)的最小值为﹣1,可得实数a,b的值;(2)若不等式f(3x)﹣t3x≥0在x∈[﹣2,2]上恒成立,t≤ ![]() 在x∈[﹣2,2]上恒成立,进而得到实数t的取值范围;(3)若关于x的方程f(|2x﹣2|)+k
在x∈[﹣2,2]上恒成立,进而得到实数t的取值范围;(3)若关于x的方程f(|2x﹣2|)+k ![]() ﹣3k=0有三个不同的实数解,则方程t2﹣(4+3k)t+(3+2k)=0有两个根,其中一个在区间(0,2)上,一个在区间[2,+∞),进而可得实数k的取值范围.
﹣3k=0有三个不同的实数解,则方程t2﹣(4+3k)t+(3+2k)=0有两个根,其中一个在区间(0,2)上,一个在区间[2,+∞),进而可得实数k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
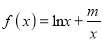 ,m∈R.
,m∈R.(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数
 零点的个数.
零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】☉O为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE为☉O的切线,求△ADE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
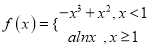 ,其中
,其中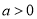 .
.(Ⅰ)求
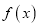 在
在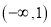 上的单调区间;
上的单调区间;(Ⅱ)求
 在
在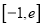 (
(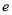 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值; -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,若
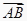 =a,
=a,  =b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
=b,且|a+b|=|a- b|,则四边形ABCD的形状是( ).
A.平行四边形
B.矩形
C.菱形
D.正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x>1},B={x|x≥2}.
(1)求集合A∩(RB);
(2)若集合C={x|x﹣a>0},且满足A∩C=C,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
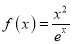 ,
, 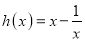 .
.(I)求函数
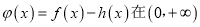 上零点的个数;
上零点的个数; (II)设
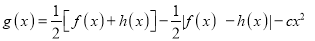 ,若函数
,若函数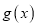 在
在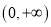 上是增函数.
上是增函数.求实数
 的取值范围.
的取值范围.
相关试题

