【题目】已知函数![]() 为定义域
为定义域![]() 上的奇函数,且在
上的奇函数,且在![]() 上是单调递增函数,函数
上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,
为等差数列,![]() ,且公差不为0,若
,且公差不为0,若![]() ,则
,则![]() ( )
( )
A. 45 B. 15 C. 10 D. 0
参考答案:
【答案】A
【解析】
根据题意,由奇函数的性质可得(-x)+f(x)=0,又由g(x)=f(x-5)+x且g(a1)+g(a2)+…+g(a9)=45,可得f(a1-5)+f(a2-5)+…+f(a9-5)+(a1+a2+…+a9)=45,结合等差数列的性质可得f(a1-5)=-f(a9-5)=f(5-a9),进而可得a1-5=5-a9,即a1+a9=10,进而计算可得答案.
根据题意,函数y=f(x)为定义域R上的奇函数,
则有f(-x)+f(x)=0,
∵g(x)=f(x-5)+x,
∴若g(a1)+g(a2)+…+g(a9)=45,
即f(a1-5)+a1+f(a2-5)+a2+…+f(a9-5)+a9=45,
即f(a1-5)+f(a2-5)+…+f(a9-5)+(a1+a2+…+a9)=45,
f(a1-5)+f(a2-5)+…+f(a9-5)=0,
又由y=f(x)为定义域R上的奇函数,且在R上是单调函数,
f(a1-5)+f(a2-5)+…+f(a9-5)是9项的和且和为0,
必有f(a1-5)+f(a9-5)=0,
则有a1-5=5-a9,
即a1+a9=10,
在等差数列中,a1+a9=10=2a5,
即a5=5,
则a1+a2+…+a9=9a5=45;
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
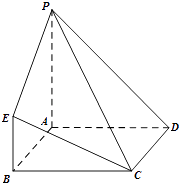
(1)求证:CE∥平面PAD;
(2)求PD与平面PCE所成角的正弦值;
(3)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 的值;如果不存在,说明理由.
的值;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】求适合下列条件的双曲线的方程:
(1) 虚轴长为12,离心率为
 ;
;(2) 焦点在x轴上,顶点间距离为6,渐近线方程为
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的中心在原点O,焦点在x轴上,离心率为
 ,椭圆C上的点到右焦点的最大距离为3.
,椭圆C上的点到右焦点的最大距离为3.
(1)求椭圆C的标准方程;
(2)斜率存在的直线l与椭圆C交于A,B两点,并且满足|2 +
+  |=|2
|=|2  ﹣
﹣  |,求直线在y轴上截距的取值范围.
|,求直线在y轴上截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
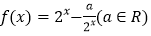 ,将
,将 的图象向右平移两个单位长度,得到函数
的图象向右平移两个单位长度,得到函数 的图象.
的图象.(1)求函数
 的解析式;
的解析式;(2)若方程
 在
在 上有且仅有一个实根,求
上有且仅有一个实根,求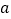 的取值范围;
的取值范围;(3)若函数
 与
与 的图象关于直线
的图象关于直线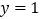 对称,设
对称,设 ,已知
,已知 对任意的
对任意的 恒成立,求
恒成立,求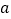 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(1﹣ax)ln(x+1)﹣bx,其中a和b是实数,曲线y=f(x)恒与x轴相切于坐标原点.
(1)求常数b的值;
(2)当a=1时,讨论函数f(x)的单调性;
(3)当0≤x≤1时关于x的不等式f(x)≥0恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设m, n是两条不同的直线,
 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A.
 ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
相关试题

