【题目】设m, n是两条不同的直线,![]() 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A. ![]() ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
参考答案:
【答案】A
【解析】
对于①,因为![]() ,所以经过
,所以经过![]() 作平面
作平面![]() ,使
,使![]() ,可得
,可得![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() ,结合
,结合![]() 得
得![]() .由此可得①是真命题;
.由此可得①是真命题;
对于②,因为![]() 且
且![]() ,所以
,所以![]() ,
,
结合![]() ,可得
,可得![]() ,故②是真命题;
,故②是真命题;
对于③,设直线![]() 、
、![]() 是位于正方体上底面所在平面内的相交直线,
是位于正方体上底面所在平面内的相交直线,
而平面![]() 是正方体下底面所在的平面,
是正方体下底面所在的平面,
则有![]() 且
且![]() 成立,但不能推出
成立,但不能推出![]() ,故③不正确;
,故③不正确;
对于④,设平面![]() 、
、![]() 、
、![]() 是位于正方体经过同一个顶点的三个面,
是位于正方体经过同一个顶点的三个面,
则有![]() 且
且![]() ,但是
,但是![]() ,推不出
,推不出![]() ,故④不正确.
,故④不正确.
综上所述,其中正确命题的序号是①和②,
故选:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数列
 是公差为2的等差数列,数列
是公差为2的等差数列,数列 满足b1=1,b2=2,且anbn+bn=nbn+1.
满足b1=1,b2=2,且anbn+bn=nbn+1.(1)求数列
 ,
, 的通项公式;
的通项公式;(2)设数列
 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 ,若不等式
,若不等式
对一切n∈N*恒成立,求实数λ的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f″(x)=0有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=2x3﹣3x2+
 ,则g(
,则g(  )+g(
)+g(  )+…+g(
)+…+g(  )=( )
)=( )
A.100
B.50
C.
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是函数
 在区间
在区间 上的图象,为了得到这个函数的图象,只需将y=sinx的图象
上的图象,为了得到这个函数的图象,只需将y=sinx的图象
A. 向左平移
 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的 ,纵坐标不变
,纵坐标不变B. 向左平移至
 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变C. 向左平移
 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的 ,纵坐标不变
,纵坐标不变D. 向左平移
 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,
,  ,设函数
,设函数 .
.(1)求函数
 的单调递增区间;
的单调递增区间;(2)在
 中,边
中,边 分别是角
分别是角 的对边,角
的对边,角 为锐角,若
为锐角,若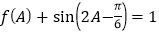 ,
,  ,
,  的面积为
的面积为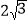 ,求边
,求边 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标





机床甲
8
12
40
32
8
机床乙
7
18
40
29
6
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在
 内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 是等腰三角形,且
是等腰三角形,且 .四边形
.四边形 是直角梯形,
是直角梯形, ,
, ,
, ,
, ,
, .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)当平面

 平面
平面 时,求四棱锥
时,求四棱锥 的体积;
的体积;(Ⅲ)请在图中所给的五个点
 中找出两个点,使得这两点所在的直线与直线
中找出两个点,使得这两点所在的直线与直线 垂直,并给出证明.
垂直,并给出证明.
相关试题

