【题目】已知函数![]() ,将
,将![]() 的图象向右平移两个单位长度,得到函数
的图象向右平移两个单位长度,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
【试题分析】(1)借助平移的知识可直接求得函数解析式;(2)先换元![]() 将问题进行等价转化为
将问题进行等价转化为![]() 有且只有一个根,再构造二次函数
有且只有一个根,再构造二次函数![]() 运用函数方程思想建立不等式组分析求解;(3)先依据题设条件求出函数的解析式
运用函数方程思想建立不等式组分析求解;(3)先依据题设条件求出函数的解析式![]() ,再运用不等式恒成立求出函数
,再运用不等式恒成立求出函数![]() 的最小值:
的最小值:
解:(1) ![]()
(2)设![]() ,则
,则![]() ,原方程可化为
,原方程可化为![]()
于是只须![]() 在
在![]() 上有且仅有一个实根,
上有且仅有一个实根,
法1:设![]() ,对称轴t=
,对称轴t=![]() ,则
,则![]() ① , 或
① , 或  ②
②
由①得 ![]() ,即
,即![]() ,
,![]()
由②得![]() 无解, ,则
无解, ,则![]() 。
。
法2:由![]()
![]() ,得,
,得,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,记
,记![]() ,
,
则![]() 在
在![]() 上是单调函数,因为故要使题设成立,
上是单调函数,因为故要使题设成立,
只须![]() ,即
,即![]() ,
,
从而有![]()
(3)设![]() 的图像上一点
的图像上一点![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
由点![]() 在
在![]() 的图像上,所以
的图像上,所以![]() ,
,
于是![]() 即
即![]() .
.![]() .
.
由![]() ,化简得
,化简得![]() ,设
,设![]() ,即
,即![]() 恒成立.
恒成立.
解法1:设![]() ,对称轴
,对称轴![]()
则![]() ③ 或
③ 或  ④
④
由③得 , 由④得
, 由④得 或
或![]() ,即
,即![]() 或
或![]()
综上,![]() .
.
解法2:注意到![]() ,分离参数得
,分离参数得![]() 对任意
对任意![]() 恒成立
恒成立
设![]() ,
,![]() ,即
,即![]()
![]()
可证![]() 在
在![]() 上单调递增
上单调递增 ![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】求适合下列条件的双曲线的方程:
(1) 虚轴长为12,离心率为
 ;
;(2) 焦点在x轴上,顶点间距离为6,渐近线方程为
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的中心在原点O,焦点在x轴上,离心率为
 ,椭圆C上的点到右焦点的最大距离为3.
,椭圆C上的点到右焦点的最大距离为3.
(1)求椭圆C的标准方程;
(2)斜率存在的直线l与椭圆C交于A,B两点,并且满足|2 +
+  |=|2
|=|2  ﹣
﹣  |,求直线在y轴上截距的取值范围.
|,求直线在y轴上截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
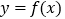 为定义域
为定义域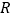 上的奇函数,且在
上的奇函数,且在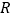 上是单调递增函数,函数
上是单调递增函数,函数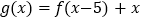 ,数列
,数列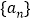 为等差数列,
为等差数列,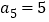 ,且公差不为0,若
,且公差不为0,若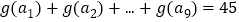 ,则
,则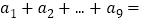 ( )
( )A. 45 B. 15 C. 10 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(1﹣ax)ln(x+1)﹣bx,其中a和b是实数,曲线y=f(x)恒与x轴相切于坐标原点.
(1)求常数b的值;
(2)当a=1时,讨论函数f(x)的单调性;
(3)当0≤x≤1时关于x的不等式f(x)≥0恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设m, n是两条不同的直线,
 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A.
 ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,圆C的方程为(x﹣
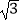 )2+(y+1)2=9,以O为极点,x轴的非负半轴为极轴建立极坐标系.
)2+(y+1)2=9,以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线OP:θ= (p∈R)与圆C交于点M,N,求线段MN的长.
(p∈R)与圆C交于点M,N,求线段MN的长.
相关试题

