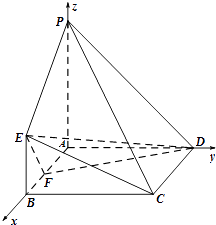
【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2. 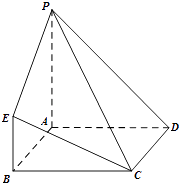
(1)求证:CE∥平面PAD;
(2)求PD与平面PCE所成角的正弦值;
(3)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
参考答案:
【答案】
(1)证明:设PA中点为G,连结EG,DG.
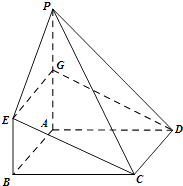
因为PA∥BE,且PA=4,BE=2,
所以BE∥AG且BE=AG,
所以四边形BEGA为平行四边形.
所以EG∥AB,且EG=AB.
因为正方形ABCD,所以CD∥AB,CD=AB,
所以EG∥CD,且EG=CD.
所以四边形CDGE为平行四边形.
所以CE∥DG.
因为DG平面PAD,CE平面PAD,
所以CE∥平面PAD.
(2)解:如图建立空间坐标系,
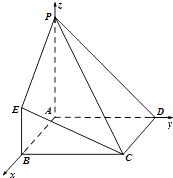
则B(4,0,0),C(4,4,0),
E(4,0,2),P(0,0,4),D(0,4,0),
所以 ![]() =(4,4,﹣4),
=(4,4,﹣4), ![]() =(4,0,﹣2),
=(4,0,﹣2), ![]() =(0,4,﹣4).
=(0,4,﹣4).
设平面PCE的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
所以 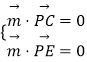 ,可得
,可得 ![]() .
.
令x=1,则 ![]() ,所以
,所以 ![]() =(1,1,2).
=(1,1,2).
设PD与平面PCE所成角为a,
则sinα=|cos< ![]() ,
, ![]() >|=|
>|=| 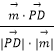 =|
=| ![]() |=
|= ![]() ..
..
所以PD与平面PCE所成角的正弦值是 ![]() .
.
(3)解:依题意,可设F(a,0,0),则 ![]() ,
, ![]() =(4,﹣4,2).
=(4,﹣4,2).
设平面DEF的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 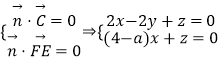 .
.
令x=2,则 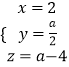 ,
,
所以 ![]() =(2,
=(2, ![]() ,a﹣4).
,a﹣4).
因为平面DEF⊥平面PCE,
所以 ![]()
![]() =0,即2+
=0,即2+ ![]() +2a﹣8=0,
+2a﹣8=0,
所以a= ![]() <4,点
<4,点 ![]() .
.
所以 ![]() .
.
【解析】(1)设PA中点为G,连结EG,DG,可证四边形BEGA为平行四边形,又正方形ABCD,可证四边形CDGE为平行四边形,得CE∥DG,由DG平面PAD,CE平面PAD,即证明CE∥平面PAD.(2)如图建立空间坐标系,设平面PCE的一个法向量为 ![]() =(x,y,z),由
=(x,y,z),由 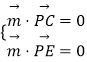 ,令x=1,则可得
,令x=1,则可得 ![]() =(1,1,2),设PD与平面PCE所成角为a,由向量的夹角公式即可得解.(3)设平面DEF的一个法向量为
=(1,1,2),设PD与平面PCE所成角为a,由向量的夹角公式即可得解.(3)设平面DEF的一个法向量为 ![]() =(x,y,z),由
=(x,y,z),由 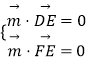 ,可得
,可得 ![]() ,由
,由 ![]()
![]() =0,可解a,然后求得
=0,可解a,然后求得 ![]() 的值.
的值.
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则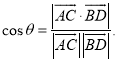 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点到准线的距离为
的焦点到准线的距离为 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点 .
.(1)若
 的坐标为
的坐标为 ,求
,求 的值;
的值;(2)设线段
 的中点为
的中点为 ,点
,点 的坐标为
的坐标为 ,过
,过 的直线
的直线 与线段
与线段 为直径的圆相切,切点为
为直径的圆相切,切点为 ,且直线
,且直线 与抛物线
与抛物线 交于
交于 两点,求
两点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄的频数分布及支持“生育二胎”人数如表:
年龄
[5,15)
[15,25)
[25,35)
[35,45)
[45,55)
[55,65)
频数
5
10
15
10
5
5
支持“生育二胎”
4
5
12
8
2
1
(1)由以上统计数据填下面2乘2列联表,并问是否有的99%把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:
(2)若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望;年龄不低于45岁的人数
年龄低于45岁的人数
合计
支持
a=
c=
不支持
b=
d=
合计
参考数据:
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
K2=
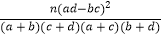 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 :实数
:实数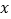 满足
满足 ,其中
,其中 ;
; :实数
:实数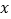 满足
满足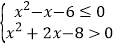 .
.(1)若
 ,且
,且 为真,
为真, 为假,求实数
为假,求实数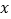 的取值范围;
的取值范围;(2)若
 是
是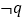 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】求适合下列条件的双曲线的方程:
(1) 虚轴长为12,离心率为
 ;
;(2) 焦点在x轴上,顶点间距离为6,渐近线方程为
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的中心在原点O,焦点在x轴上,离心率为
 ,椭圆C上的点到右焦点的最大距离为3.
,椭圆C上的点到右焦点的最大距离为3.
(1)求椭圆C的标准方程;
(2)斜率存在的直线l与椭圆C交于A,B两点,并且满足|2 +
+  |=|2
|=|2  ﹣
﹣  |,求直线在y轴上截距的取值范围.
|,求直线在y轴上截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
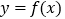 为定义域
为定义域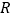 上的奇函数,且在
上的奇函数,且在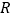 上是单调递增函数,函数
上是单调递增函数,函数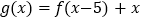 ,数列
,数列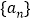 为等差数列,
为等差数列,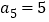 ,且公差不为0,若
,且公差不为0,若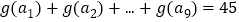 ,则
,则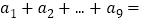 ( )
( )A. 45 B. 15 C. 10 D. 0
相关试题

