【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在整数
;(2)存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值.
上存在极小值.
【解析】
试题分析:(1)由![]()
![]()
![]() ,设
,设![]() ,则
,则![]() ,利用导数工具求得
,利用导数工具求得![]() ,原命题可转化为
,原命题可转化为![]() 对
对![]() 恒成立
恒成立![]()
![]()
![]()
![]() 的取值范围为
的取值范围为![]() ;(2)易得
;(2)易得![]()
![]()
![]() ,利用分类讨论思想对
,利用分类讨论思想对![]() 、
、![]() 和
和![]() 分三种情况可得:存在整数
分三种情况可得:存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值.
上存在极小值.
试题解析:(1)由![]() 得
得![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,∴
,∴![]() ,则
,则![]() 在
在![]() 上是减函数,
上是减函数,
∴![]() ,
,
![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,
恒成立,
∴![]() ,则实数
,则实数![]() 的取值范围为
的取值范围为![]() .
.
(2)![]() ,
,
∴![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 单调递增,无极值.
单调递增,无极值.
②当![]() 时,若
时,若![]() ,或
,或![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
∴当![]() 时,有极小值.
时,有极小值.
![]() 在
在![]() 上有极小值,∴
上有极小值,∴![]() .∴存在整数
.∴存在整数![]() .
.
③当![]() 时,若
时,若![]() 或
或![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() .
.
∴当![]() 时,
时,![]() 有极小值.
有极小值.
![]() 在
在![]() 上有极小值,
上有极小值,
∴![]() ,得
,得![]() .
.
由①②③得,存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值.
上存在极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x-1|+|x+1|(x∈R).
(1)证明:函数f(x)是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图象;
(3)写出函数的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABCA1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
 .
.(1)求证:C1B⊥平面ABC;
设
 (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届河北省正定中学高三上学期第三次月考(期中)数学(理)】在平面直角坐标系中,当
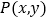 不是原点时,定义
不是原点时,定义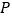 的“伴随点”为
的“伴随点”为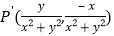 ;当
;当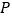 是原点时,定义
是原点时,定义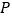 的“伴随点”为它自身,平面曲线
的“伴随点”为它自身,平面曲线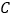 上所有点的“伴随点”所构成的曲线
上所有点的“伴随点”所构成的曲线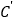 定义为曲线
定义为曲线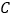 的“伴随曲线”,现有下列命题:
的“伴随曲线”,现有下列命题:①若点
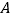 的“伴随点”是点
的“伴随点”是点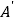 ,则点
,则点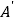 的“伴随点”是点
的“伴随点”是点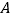 ;
;②若曲线
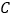 关于
关于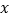 轴对称,则其“伴随曲线”
轴对称,则其“伴随曲线” 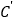 关于
关于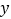 轴对称;
轴对称;③单位圆的“伴随曲线”是它自身;
④一条直线的“伴随曲线”是一条直线.
其中真命题的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线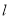 的参数方程为
的参数方程为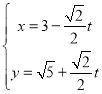 (
(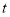 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系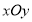 取相同的长度单位,且以原点
取相同的长度单位,且以原点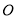 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为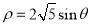 .
.(1)求圆
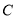 的直角坐标方程;
的直角坐标方程;(2)设圆
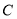 与直线
与直线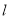 交于点
交于点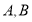 ,若点
,若点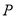 的坐标为
的坐标为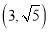 ,求
,求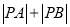 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2014山东.理15】已知函数
 ,对函数
,对函数 ,定义
,定义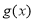 关于
关于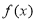 的对称函数为函数
的对称函数为函数 ,
, 满足:对于任意
满足:对于任意 ,两个点
,两个点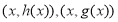 关于点
关于点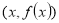 对称,若
对称,若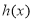 是
是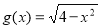 关于
关于 的“对称函数”,且
的“对称函数”,且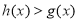 恒成立,则实数
恒成立,则实数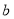 的取值范围是_________.
的取值范围是_________. -
科目: 来源: 题型:
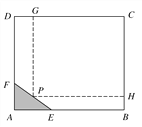
查看答案和解析>>【题目】如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,问如何设计才能使公园占地面积最大,求出最大面积.
相关试题

