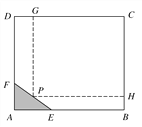
【题目】如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,问如何设计才能使公园占地面积最大,求出最大面积.
参考答案:
【答案】详见解析.
【解析】试题分析: 在EF上取一点P,作PH⊥BC,PG⊥CD,垂足分别为H、G,设PH=x,则140≤x≤200.
由三角形相似得出PG用x表示,进而得出公园占地面积关于x的函数,用配方法得出函数的最值,以及取到最值时的x值.
试题解析:
如题图,在EF上取一点P,作PH⊥BC,PG⊥CD,垂足分别为H、G,设PH=x,则140≤x≤200.
由三角形相似性质PG=120+![]() (200-x),
(200-x),
∴公园占地面积为S=x[120+![]() (200-x)]
(200-x)]
=-![]() x2+
x2+![]() x
x
=-![]() (x-190)2+
(x-190)2+![]() ×1902(140≤x≤200),
×1902(140≤x≤200),
∴当x=190时,Smax=![]() m2.
m2.
答:在EF上取一点P,使P到BC距离为190m时,公园PHCG占地面积最大,最大面积为![]() m2.
m2.
点睛: 本题考查函数的实际应用问题,解决问题的关键是利用相似求出函数的解析式,用二次函数的单调性解决函数的最值.解决函数模型应用的解答题,还有以下几点容易造成失分:①读不懂实际背景,不能将实际问题转化为函数模型.②对涉及的相关公式,记忆错误.③在求解的过程中计算错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
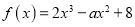 .
.(1)若
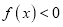 对
对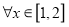 恒成立,求实数
恒成立,求实数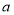 的取值范围;
的取值范围;(2)是否存在整数
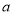 ,使得函数
,使得函数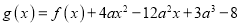 在区间
在区间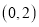 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数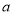 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线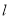 的参数方程为
的参数方程为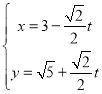 (
(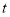 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系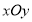 取相同的长度单位,且以原点
取相同的长度单位,且以原点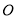 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为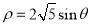 .
.(1)求圆
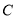 的直角坐标方程;
的直角坐标方程;(2)设圆
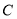 与直线
与直线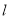 交于点
交于点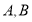 ,若点
,若点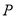 的坐标为
的坐标为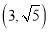 ,求
,求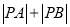 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2014山东.理15】已知函数
 ,对函数
,对函数 ,定义
,定义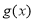 关于
关于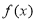 的对称函数为函数
的对称函数为函数 ,
, 满足:对于任意
满足:对于任意 ,两个点
,两个点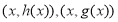 关于点
关于点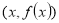 对称,若
对称,若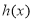 是
是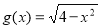 关于
关于 的“对称函数”,且
的“对称函数”,且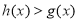 恒成立,则实数
恒成立,则实数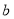 的取值范围是_________.
的取值范围是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】罗源滨海新城建一座桥,两端的桥墩已建好,这两墩相距
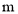 米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米的相邻两墩之间的桥面工程费用为
米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米的相邻两墩之间的桥面工程费用为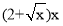 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为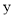 万元.
万元.(1)试写出
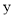 关于
关于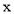 的函数关系式;
的函数关系式;(2)当
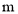 =96米,需新建多少个桥墩才能使余下工程的费用
=96米,需新建多少个桥墩才能使余下工程的费用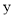 最小?
最小? -
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费用支出
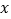 与销售额
与销售额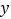 之间有如下的对应数据:
之间有如下的对应数据: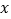
2
4
5
6
8
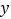
30
40
60
50
70
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程
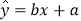 ;
;(3)据此估计广告费用为10时,销售收入
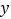 的值.
的值.(参考公式:
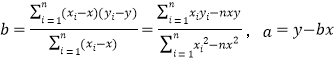 ,).
,). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合P={x|-2≤x≤10},Q={x|1-m≤x≤1+m}.
(1)求集合RP;
(2)若PQ,求实数m的取值范围;
(3)若P∩Q=Q,求实数m的取值范围.
相关试题

