【题目】已知函数f(x)=|x-1|+|x+1|(x∈R).
(1)证明:函数f(x)是偶函数;
(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图象;
(3)写出函数的值域.
参考答案:
【答案】(1)见解析(2)见解析(3)[2,+∞).
【解析】试题分析:(1)先确定定义域关于原点对称,再根据f(-x)与f(x)相等得偶函数(2)根据绝对值定义将函数分成三段,通过描点画函数图像(3)根据函调图像可得函数最小值,无最大值,即得函数值域
试题解析:解: (1)证明:∵f(-x)=|-x-1|+|-x+1|=|-(x+1)|+|-(x-1)|=|x+1|+|x-1|=f(x),
∴函数f(x)=|x-1|+|x+1|(x∈R)为偶函数.
 (2)由x-1=0,得x=1;由x+1=0,得x=-1.
(2)由x-1=0,得x=1;由x+1=0,得x=-1.
当x<-1时,f(x)=-2x;
当-1≤x≤1时,f(x)=2;
当x>1时,f(x)=2x.
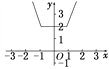
∴f(x)=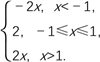 f(x)的图象如图所示.
f(x)的图象如图所示.
(3)由函数图象知,函数的值域为[2,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2016高考四川文科】已知数列{
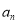 }的首项为1,
}的首项为1,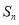 为数列
为数列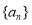 的前n项和,
的前n项和,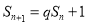 ,其中q>0,
,其中q>0, .
.(Ⅰ)若
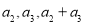 成等差数列,求
成等差数列,求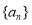 的通项公式;
的通项公式;(Ⅱ)设双曲线
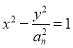 的离心率为
的离心率为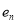 ,且
,且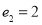 ,求
,求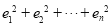 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
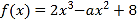 .
.(1)若
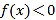 对
对 恒成立,求实数
恒成立,求实数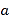 的取值范围;
的取值范围;(2)是否存在整数
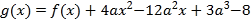 ,使得函数
,使得函数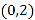 在区间
在区间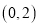 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数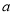 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设全集U=R,集合A={x|y=
 },B={x|x2-x-6=0}.
},B={x|x2-x-6=0}.(1)若a=-1,求A∩B;
(2)若(
 )∩B=,求实数a的取值范围.
)∩B=,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABCA1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
 .
.(1)求证:C1B⊥平面ABC;
设
 (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届河北省正定中学高三上学期第三次月考(期中)数学(理)】在平面直角坐标系中,当
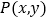 不是原点时,定义
不是原点时,定义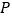 的“伴随点”为
的“伴随点”为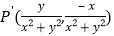 ;当
;当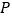 是原点时,定义
是原点时,定义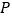 的“伴随点”为它自身,平面曲线
的“伴随点”为它自身,平面曲线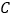 上所有点的“伴随点”所构成的曲线
上所有点的“伴随点”所构成的曲线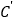 定义为曲线
定义为曲线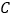 的“伴随曲线”,现有下列命题:
的“伴随曲线”,现有下列命题:①若点
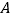 的“伴随点”是点
的“伴随点”是点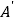 ,则点
,则点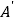 的“伴随点”是点
的“伴随点”是点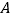 ;
;②若曲线
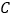 关于
关于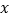 轴对称,则其“伴随曲线”
轴对称,则其“伴随曲线” 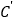 关于
关于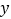 轴对称;
轴对称;③单位圆的“伴随曲线”是它自身;
④一条直线的“伴随曲线”是一条直线.
其中真命题的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
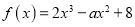 .
.(1)若
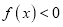 对
对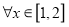 恒成立,求实数
恒成立,求实数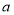 的取值范围;
的取值范围;(2)是否存在整数
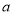 ,使得函数
,使得函数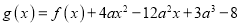 在区间
在区间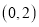 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数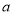 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

