【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为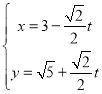 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)在![]() 两边同乘以
两边同乘以![]() ,则有
,则有![]() ,即
,即![]() 这就是圆
这就是圆![]() 的直角坐标方程;(2)方法一:把
的直角坐标方程;(2)方法一:把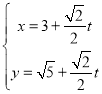 代入
代入![]()
![]()
![]()
![]()
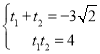
![]()
![]()
![]() .方法二:联立方程组求得
.方法二:联立方程组求得
![]() ,又点
,又点![]() 的坐标为
的坐标为![]() ,故
,故![]() .
.
试题解析:(1)方法一:(1)由![]() ,
,
得![]() ,即
,即![]() ;
;
(2)将![]() 的参数方程代入圆
的参数方程代入圆![]() 的直角坐标方程,得
的直角坐标方程,得
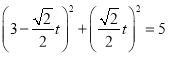 ,即
,即![]() ,
,
由于![]() ,
,
故可设![]() 是上述方程的两实根,
是上述方程的两实根,
所以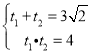 ,又直线
,又直线![]() 过点
过点![]() ,故由上式及
,故由上式及![]() 的几何意义得
的几何意义得
![]() .
.
方法二:(1)同方法一.
(2)因为圆![]() 的圆心为点
的圆心为点![]() ,半径
,半径![]() ,直线
,直线![]() 的普通方程为
的普通方程为![]() ,
,
由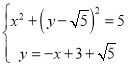 得
得![]() ,
,
解得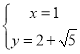 或
或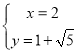 ,
,
不妨设![]() ,又点
,又点![]() 的坐标为
的坐标为![]() ,
,
故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABCA1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
 .
.(1)求证:C1B⊥平面ABC;
设
 (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届河北省正定中学高三上学期第三次月考(期中)数学(理)】在平面直角坐标系中,当
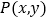 不是原点时,定义
不是原点时,定义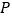 的“伴随点”为
的“伴随点”为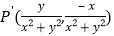 ;当
;当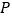 是原点时,定义
是原点时,定义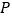 的“伴随点”为它自身,平面曲线
的“伴随点”为它自身,平面曲线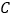 上所有点的“伴随点”所构成的曲线
上所有点的“伴随点”所构成的曲线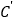 定义为曲线
定义为曲线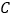 的“伴随曲线”,现有下列命题:
的“伴随曲线”,现有下列命题:①若点
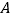 的“伴随点”是点
的“伴随点”是点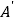 ,则点
,则点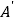 的“伴随点”是点
的“伴随点”是点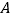 ;
;②若曲线
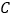 关于
关于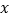 轴对称,则其“伴随曲线”
轴对称,则其“伴随曲线” 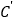 关于
关于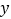 轴对称;
轴对称;③单位圆的“伴随曲线”是它自身;
④一条直线的“伴随曲线”是一条直线.
其中真命题的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
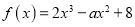 .
.(1)若
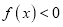 对
对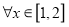 恒成立,求实数
恒成立,求实数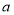 的取值范围;
的取值范围;(2)是否存在整数
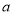 ,使得函数
,使得函数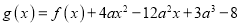 在区间
在区间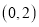 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数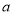 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2014山东.理15】已知函数
 ,对函数
,对函数 ,定义
,定义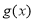 关于
关于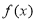 的对称函数为函数
的对称函数为函数 ,
, 满足:对于任意
满足:对于任意 ,两个点
,两个点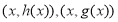 关于点
关于点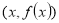 对称,若
对称,若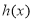 是
是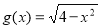 关于
关于 的“对称函数”,且
的“对称函数”,且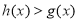 恒成立,则实数
恒成立,则实数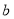 的取值范围是_________.
的取值范围是_________. -
科目: 来源: 题型:
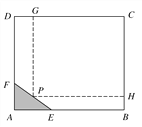
查看答案和解析>>【题目】如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,问如何设计才能使公园占地面积最大,求出最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】罗源滨海新城建一座桥,两端的桥墩已建好,这两墩相距
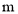 米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米的相邻两墩之间的桥面工程费用为
米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米的相邻两墩之间的桥面工程费用为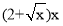 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为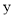 万元.
万元.(1)试写出
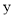 关于
关于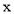 的函数关系式;
的函数关系式;(2)当
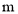 =96米,需新建多少个桥墩才能使余下工程的费用
=96米,需新建多少个桥墩才能使余下工程的费用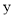 最小?
最小?
相关试题

