【题目】已知圆![]() :
: ![]() 过椭圆
过椭圆![]() :
: ![]() (
(![]() )的短轴端点,
)的短轴端点, ![]() ,
, ![]() 分别是圆
分别是圆![]() 与椭圆
与椭圆![]() 上任意两点,且线段
上任意两点,且线段![]() 长度的最大值为3.
长度的最大值为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作圆
作圆![]() 的一条切线交椭圆
的一条切线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的面积的最大值.
的面积的最大值.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)1.
(Ⅱ)1.
【解析】试题分析: (Ⅰ)根据椭圆几何性质得线段![]() 长度的最大值为
长度的最大值为![]() ,且
,且![]() ,解出
,解出![]() ,得椭圆
,得椭圆![]() 的方程;(Ⅱ)利用点斜式设直线方程,与椭圆方程联立,结合韦达定理及弦长公式可得底边
的方程;(Ⅱ)利用点斜式设直线方程,与椭圆方程联立,结合韦达定理及弦长公式可得底边![]() 长(用斜率及
长(用斜率及![]() 表示);利用点到直线距离公式得三角形的高(用斜率及
表示);利用点到直线距离公式得三角形的高(用斜率及![]() 表示);根据圆心到切线距离等于半径得斜率与
表示);根据圆心到切线距离等于半径得斜率与![]() 关系,代入面积公式并化简得关于
关系,代入面积公式并化简得关于![]() 的函数关系式,最后利用基本不等式求最值.
的函数关系式,最后利用基本不等式求最值.
试题解析:解:(Ⅰ)∵圆![]() 过椭圆
过椭圆![]() 的短轴端点,∴
的短轴端点,∴![]() ,又∵线段
,又∵线段![]() 长度的最大值为3,
长度的最大值为3,
∴![]() ,即
,即![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)由题意可设切线![]() 的方程为
的方程为![]() ,即
,即![]() ,则
,则![]() ,得
,得![]() .①
.①
联立得方程组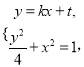 消去
消去![]() 整理得
整理得![]() .
.
其中![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
则![]() .②
.②
将①代入②得![]() ,∴
,∴![]() ,
,
而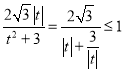 ,等号成立当且仅当
,等号成立当且仅当![]() ,即
,即![]() .
.
综上可知: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照
 ,
,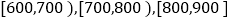 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.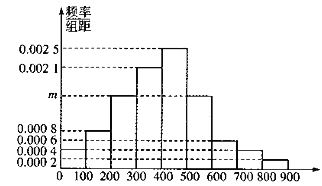
(1)求直方图中
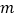 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用
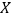 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量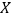 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市将建一个制药厂,但该厂投产后预计每天要排放大约80吨工业废气,这将造成极大的环境污染.为了保护环境,市政府决定支持该厂贷款引进废气处理设备来减少废气的排放,该设备可以将废气转化为某种化工产品和符合排放要求的气体,经测算,制药厂每天利用设备处理废气的综合成本
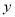 (元)与废气处理量
(元)与废气处理量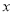 (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为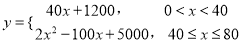 ,且每处理
,且每处理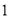 吨工业废气可得价值为
吨工业废气可得价值为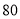 元的某种化工产品并将之利润全部用来补贴废气处理.
元的某种化工产品并将之利润全部用来补贴废气处理.(1)若该制药厂每天废气处理量计划定位20吨时,那么工厂需要每天投入的废气处理资金为多少元?
(2)若该制药厂每天废气处理量计划定为
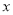 吨,且工厂不用投入废气处理资金就能完成计划的处理量,求
吨,且工厂不用投入废气处理资金就能完成计划的处理量,求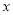 的取值范围;
的取值范围;(3)若该制药厂每天废气处理量计划定为
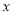 (
(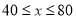 )吨,且市政府决定为处理每吨废气至少补贴制药厂
)吨,且市政府决定为处理每吨废气至少补贴制药厂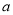 元以确保该厂完成计划的处理量总是不用投入废气处理资金,求
元以确保该厂完成计划的处理量总是不用投入废气处理资金,求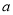 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015男篮亚锦赛决赛阶段,中国男篮以9连胜的不败战绩赢得第28届亚锦赛冠军,同时拿到亚洲唯一1张直通里约奥运会的入场券,赛后,中国男篮主力易建联荣膺本届亚锦赛
 (最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.
(最有价值球员),下表是易建联在这9场比赛中投篮的统计数据.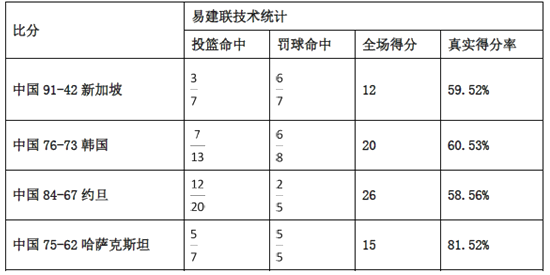
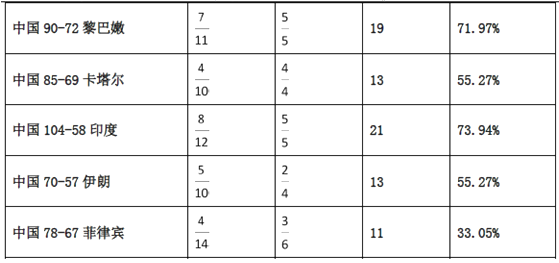
注:(1)表中
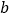 表示出手
表示出手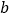 次命中
次命中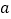 次;
次;(2)
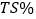 (真实得分率)是衡量球员进攻的效率,其计算公式为:
(真实得分率)是衡量球员进攻的效率,其计算公式为:
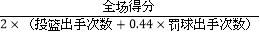
(1)从上述9场比赛中随机选择一场,求易建联在该场比赛中
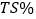 超过50%的概率;
超过50%的概率;(2)从上述9场比赛中随机选择一场,求易建联在该场比赛中
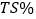 至少有一场超过60%的概率;
至少有一场超过60%的概率;(3)用
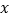 来表示易建联某场的得分,用
来表示易建联某场的得分,用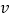 来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断
来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断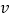 与
与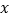 之间是否具有线性相关关系?结合实际简单说明理由.
之间是否具有线性相关关系?结合实际简单说明理由.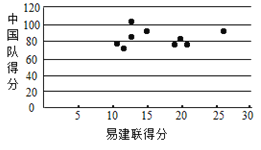
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数f(x)=xα,当x>1时,恒有f(x)<x,则α的取值范围是( )
A. (0,1) B. (-∞,1)
C. (0,+∞) D. (-∞,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中有四个小球,分别写有“幸”“福”“快”“乐”四个字,有放回地从中任取一个小球,取到“快”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止的概率为( )
A.
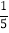 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
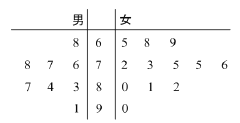
查看答案和解析>>【题目】某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示.成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
(Ⅰ)求出8名男生的平均成绩和12 名女生成绩的中位数;
(Ⅱ)按照获奖类型,用分层抽样的方法从这20名学生中抽取5人,再从选出的5人中任选3人,求恰有1人获“优秀奖”的概率.
相关试题

