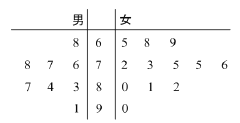
【题目】某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示.成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
(Ⅰ)求出8名男生的平均成绩和12 名女生成绩的中位数;
(Ⅱ)按照获奖类型,用分层抽样的方法从这20名学生中抽取5人,再从选出的5人中任选3人,求恰有1人获“优秀奖”的概率.
参考答案:
【答案】(I)平均数为![]() ,中位数为
,中位数为![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(Ⅰ)由平均数及中位数的概念,根据茎叶图可得结果;(Ⅱ)由茎叶图可知,获“纪念奖”的有12人,获“优秀奖”的有8人.用分层抽样的方法从中抽取5人,则“纪念奖”抽取![]() 人,“优秀奖”有2人,利用列举法及古典概型计算公式可求出结果.
人,“优秀奖”有2人,利用列举法及古典概型计算公式可求出结果.
试题解析:
解:(Ⅰ)8名男生的平均成绩为:
![]() .
.
12 名女生成绩的中位数为75.
(Ⅱ)由茎叶图可知,获“纪念奖”的有12人,获“优秀奖”的有8人.用分层抽样的方法从中抽取5人,则“纪念奖”抽取![]() 人,分别记为
人,分别记为![]() ,“优秀奖”有2人,分别记为
,“优秀奖”有2人,分别记为![]() .
.
从这5 人中选取3 人,所有结果有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10个.这些事件的出现是等可能的.
共10个.这些事件的出现是等可能的.
恰有人获“优秀奖”的结果有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6个.
,共6个.
所以,选出的3人中恰有1人获“优秀奖”的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
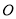 :
: 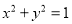 过椭圆
过椭圆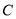 :
: 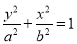 (
(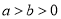 )的短轴端点,
)的短轴端点, 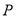 ,
, 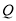 分别是圆
分别是圆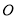 与椭圆
与椭圆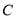 上任意两点,且线段
上任意两点,且线段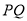 长度的最大值为3.
长度的最大值为3.(Ⅰ)求椭圆
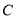 的方程;
的方程;(Ⅱ)过点
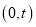 作圆
作圆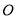 的一条切线交椭圆
的一条切线交椭圆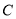 于
于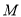 ,
, 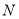 两点,求
两点,求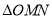 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数f(x)=xα,当x>1时,恒有f(x)<x,则α的取值范围是( )
A. (0,1) B. (-∞,1)
C. (0,+∞) D. (-∞,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中有四个小球,分别写有“幸”“福”“快”“乐”四个字,有放回地从中任取一个小球,取到“快”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止的概率为( )
A.
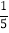 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)设
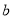 和
和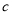 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量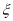 表示方程
表示方程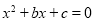 实根的个数(重根按一个计).
实根的个数(重根按一个计).(Ⅰ)求方程
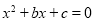 有实根的概率;
有实根的概率;(Ⅱ)求
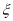 的分布列和数学期望;
的分布列和数学期望;(Ⅲ)求在先后两次出现的点数中有5的条件下,方程
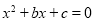 有实根的概率.
有实根的概率. -
科目: 来源: 题型:
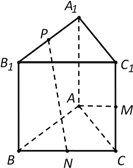
查看答案和解析>>【题目】如图,直三棱柱ABC-A1B1C1中, AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角
最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某射击运动员每次击中目标的概率都是0.8.现采用随机模拟的方法估计该运动员射击4次,至多击中1次的概率:先由计算器产生0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
5 727 0 293 7 140 9 857 0 347
4 373 8 636 9 647 1 417 4 698
0 371 6 233 2 616 8 045 6 011
3 661 9 597 7 424 6 710 4 281
据此估计,该射击运动员射击4次至多击中1次的概率为( )
A. 0.95 B. 0.1
C. 0.15 D. 0.05
相关试题

