【题目】为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部分在该市随机调查了![]() 户居民六月份的用电量(单位:
户居民六月份的用电量(单位:![]() )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
用电量数据如下:
![]() .
.
对应的家庭收入数据如下:
![]()
![]() .
.
(Ⅰ)根据国家发改委的指示精神,该市计划实施![]() 阶阶梯电价,使
阶阶梯电价,使![]() 的用户在第一档,电价为
的用户在第一档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第二档,电价为
的用户在第二档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第三档,电价为
的用户在第三档,电价为![]() 元/
元/![]() ,试求出居民用电费用
,试求出居民用电费用![]() 与用电量
与用电量![]() 间的函数关系;
间的函数关系;
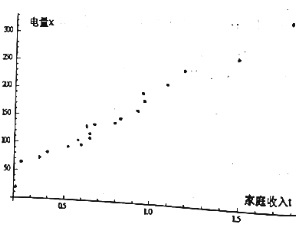
(Ⅱ)以家庭收入![]() 为横坐标,电量
为横坐标,电量![]() 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求![]() 关于
关于![]() 的回归直线方程(回归直线方程的系数四舍五入保留整数).
的回归直线方程(回归直线方程的系数四舍五入保留整数).
(Ⅲ)小明家的月收入![]() 元,按上述关系,估计小明家月支出电费多少元?
元,按上述关系,估计小明家月支出电费多少元?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:一组相关数据![]() ,
,![]() ,…,
,…,![]() 的回归直线方程
的回归直线方程![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为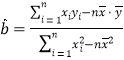 ,
,![]() ,其中
,其中![]() ,
,![]() 为样本均值.
为样本均值.
参考答案:
【答案】(1)  .
.
(2) ![]() .
.
(3) 72.8元.
【解析】分析:(Ⅰ)![]()
![]() ,
,![]() 从用电量数据中得到第一档的临界值为第15个样本,即180,第二档的临界值为第19个样本,即260.从而可得居民用电费用
从用电量数据中得到第一档的临界值为第15个样本,即180,第二档的临界值为第19个样本,即260.从而可得居民用电费用![]() 与用电量
与用电量![]() 间的函数关系;
间的函数关系;
(Ⅱ)根据题意,![]() ,
,![]() ,代入公式计算即可;
,代入公式计算即可;
(Ⅲ)代入回归直线方程即可.
详解:(I)因为![]() ,
,
所以从用电量数据中得到第一档的临界值为第15个样本,即180,
第二档的临界值为第19个样本,即260.因此,

所以,
(II)由于![]() ,
,
![]() ,
,
 ,
,
所以![]() ,
,
从而回归直线方程为![]() .
.
(Ⅲ)当![]() 时,
时,![]() ,
,
![]() ,所以,小明家月支出电费72.8元.
,所以,小明家月支出电费72.8元.
温馨提示:由于学生手工计算,难免会产生这样或那样的计算误差,望评卷老师酌情扣分。建议第(Ⅰ)问0误差,第(Ⅱ)问误差控制在±3,第(Ⅲ)问0误差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=asinθ,直线l的参数方程是
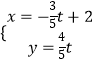 (t为参数)
(t为参数)
(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;
(2)直线l被圆C截得的弦长等于圆C的半径的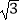 倍,求a的值.
倍,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 底面
底面 ,底面
,底面 为矩形,
为矩形, 为
为 的中点,且
的中点,且 ,
, ,
, .
.
(1)求证:
 平面
平面 ;
;(2)若点
 为线段
为线段 上一点,且
上一点,且 ,求四棱锥
,求四棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a、b满足:a>0,b>0.
(1)若x∈R,求证:|x+a|+|x﹣b|≥2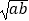 .
.
(2)若a+b=1,求证: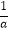 +
+  +
+ 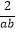 ≥12.
≥12. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;(Ⅱ)设
 ,证明:对任意
,证明:对任意 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的焦距为
的焦距为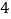 ,且过点
,且过点 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设
 为椭圆
为椭圆 上一点,过点
上一点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 .取点
.取点 ,连接
,连接 ,过点
,过点 作
作 的垂线交
的垂线交 轴于点
轴于点 .点
.点 是点
是点 关于
关于 轴的对称点,作直线
轴的对称点,作直线 ,问这样作出的直线
,问这样作出的直线 是否与椭圆
是否与椭圆 一定有唯一的公共点?并说明理由.
一定有唯一的公共点?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,圆
中,圆 的参数方程为
的参数方程为 (
( 为参数).在极坐标系(与平面直角坐标系
为参数).在极坐标系(与平面直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线 的方程为
的方程为 .
.(Ⅰ)求圆
 的普通方程及直线
的普通方程及直线 的直角坐标方程;
的直角坐标方程;(Ⅱ)设平面直角坐标系
 中的点
中的点 ,经过点
,经过点 倾斜角为
倾斜角为 的直线
的直线 与
与 相交于
相交于 ,
, 两点,求
两点,求 的取值范围.
的取值范围.
相关试题

