【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在极坐标系(与平面直角坐标系
为参数).在极坐标系(与平面直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求圆![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设平面直角坐标系![]() 中的点
中的点![]() ,经过点
,经过点![]() 倾斜角为
倾斜角为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() .
.![]() .
.
(2) ![]() .
.
【解析】分析:(Ⅰ)消去参数t得圆C的普通方程;利用极坐标与直角坐标的转化公式即可得直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)利用参数方程参数t的几何意义即可.
详解:(Ⅰ)消去参数t得圆C的普通方程为![]() .
.
由![]() ,得
,得![]() ,即
,即![]()
∴直线![]() 的直角坐标方程
的直角坐标方程![]() .
.
(Ⅱ)设直线L的方程为![]() (
(![]() 为参数),
为参数),
代入圆C的方程得![]() .
.
由t的几何意义可知,![]() ,
,
![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
因此,![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部分在该市随机调查了
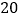 户居民六月份的用电量(单位:
户居民六月份的用电量(单位: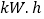 )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.用电量数据如下:
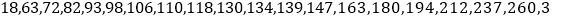 .
.对应的家庭收入数据如下:
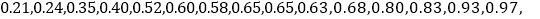
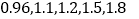 .
.
(Ⅰ)根据国家发改委的指示精神,该市计划实施
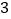 阶阶梯电价,使
阶阶梯电价,使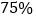 的用户在第一档,电价为
的用户在第一档,电价为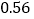 元/
元/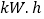 ;
;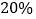 的用户在第二档,电价为
的用户在第二档,电价为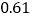 元/
元/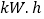 ;
;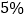 的用户在第三档,电价为
的用户在第三档,电价为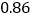 元/
元/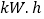 ,试求出居民用电费用
,试求出居民用电费用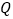 与用电量
与用电量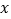 间的函数关系;
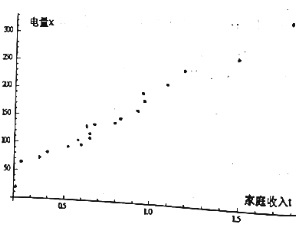
间的函数关系;(Ⅱ)以家庭收入
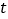 为横坐标,电量
为横坐标,电量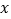 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求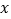 关于
关于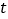 的回归直线方程(回归直线方程的系数四舍五入保留整数).
的回归直线方程(回归直线方程的系数四舍五入保留整数).(Ⅲ)小明家的月收入
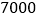 元,按上述关系,估计小明家月支出电费多少元?
元,按上述关系,估计小明家月支出电费多少元?参考数据:
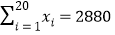 ,
,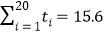 ,
,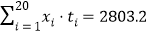 ,
,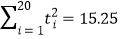 ,
,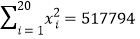 .
.参考公式:一组相关数据
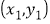 ,
,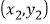 ,…,
,…,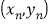 的回归直线方程
的回归直线方程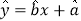 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为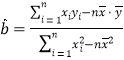 ,
,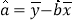 ,其中
,其中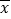 ,
,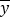 为样本均值.
为样本均值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;(Ⅱ)设
 ,证明:对任意
,证明:对任意 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的焦距为
的焦距为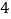 ,且过点
,且过点 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设
 为椭圆
为椭圆 上一点,过点
上一点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 .取点
.取点 ,连接
,连接 ,过点
,过点 作
作 的垂线交
的垂线交 轴于点
轴于点 .点
.点 是点
是点 关于
关于 轴的对称点,作直线
轴的对称点,作直线 ,问这样作出的直线
,问这样作出的直线 是否与椭圆
是否与椭圆 一定有唯一的公共点?并说明理由.
一定有唯一的公共点?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
 ﹣
﹣ 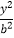 =1(a>0,b>0)的左焦点为F,离心率为
=1(a>0,b>0)的左焦点为F,离心率为  .若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
A.
=1
B.
=1
C.
=1
D.
=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,那么下列结论中错误的是( )
,那么下列结论中错误的是( )A. 若
 是
是 的极小值点,则
的极小值点,则 在区间
在区间 上单调递减
上单调递减B.
 ,使
,使
C. 函数
 的图像可以是中心对称图形
的图像可以是中心对称图形D. 若
 是
是 的极值点,则
的极值点,则
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知
 ,
, ,动点
,动点 满足
满足 ,设动点
,设动点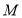 的轨迹为曲线
的轨迹为曲线 .
.(1)求动点
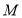 的轨迹方程,并说明曲线
的轨迹方程,并说明曲线 是什么图形;
是什么图形;(2)过点
 的直线
的直线 与曲线
与曲线 交于
交于 两点,若
两点,若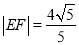 ,求直线
,求直线 的方程;
的方程;(3)设
 是直线
是直线 上的点,过
上的点,过 点作曲线
点作曲线 的切线
的切线 ,切点为
,切点为 ,设
,设 ,求证:过
,求证:过 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
相关试题

