【题目】某班主任对该班22名学生进行了作业量的调查,在喜欢玩电脑游戏的12人中,有10人认为作业多,2人认为作业不多;在不喜欢玩电脑游戏的10人中,有3人认为作业多,7人认为作业不多.
(1)根据以上数据建立一个![]() 列联表.
列联表.
(2)对于该班学生,能否在犯错误概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关系?
下面临界值表仅供参考:
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考公式:![]() .
.
参考答案:
【答案】(1)答案见解析;(2)答案见解析.
【解析】分析:(1)由题意补充![]() 列联表;
列联表;
(2)计算![]() ,查表下结论即可.
,查表下结论即可.
详解:(1)、列联表为:
认为作业多 | 认为作业不多 | 合计 | |
喜欢电脑 | 10 | 2 | 12 |
不喜欢电脑 | 3 | 7 | 10 |
合计 | 13 | 9 | 22 |
(2)、由表中数据得K2的观测值k![]()
![]()
![]()
![]() ≈6.418<6.635
≈6.418<6.635
所以,据此统计有不能在犯错误概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知F1 , F2是椭圆C:
 +
+  =1的左、右焦点.
=1的左、右焦点.
(1)若点M在椭圆C上,且∠F1MF2=60°,求△F1MF2的面积;
(2)动直线y=k(x+1)与椭圆C相交于A,B两点,点T(t,0),问是否存在t∈R,使得
 为定值,若存在求出t的值,若不存在,请说明理由.
为定值,若存在求出t的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列两个命题:
 函数
函数 在[2,+∞)单调递增;
在[2,+∞)单调递增;  关于
关于 的不等式
的不等式 的解集为
的解集为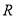 .若
.若 为真命题,
为真命题,  为假命题,求
为假命题,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,任取两个不相等的正数
,任取两个不相等的正数 ,
,  ,总有
,总有 ,对于任意的
,对于任意的 ,总有
,总有 ,若
,若 有两个不同的零点,则正实数
有两个不同的零点,则正实数 的取值范围为__________.
的取值范围为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:数列{an}中,
 =n,a2=6,n∈N+ .
=n,a2=6,n∈N+ .
(1)求a1 , a3 , a4;
(2)猜想an的表达式并给出证明;
(3)记:Sn= +
+  +…+
+…+  ,证明:Sn<
,证明:Sn<  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=
 .
. 
(1)求证:平面PQB⊥平面PAD;
(2)若PM=3MC,求二面角M﹣BQ﹣C的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】一口袋中装有大小相同的2个白球和4个黑球,每次从袋中任意摸出一个球 .
(1)采取有放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的均值和方差.
相关试题

