【题目】从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
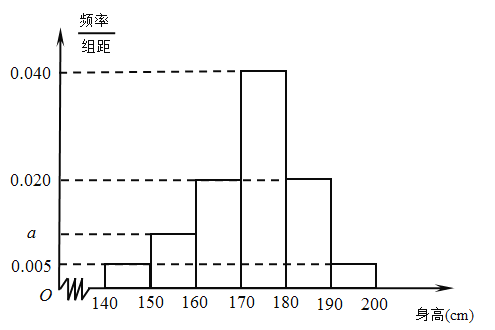
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)假设同组中的每个数据用该组区间的中点值代替,估计该市中学生中的全体男生的平均身高;
(Ⅲ)从该市的中学生中随机抽取一名男生,根据直方图中的信息,估计其身高在180 cm 以上的概率.若从全市中学的男生(人数众多)中随机抽取![]() 人,用
人,用![]() 表示身高在
表示身高在![]() 以上的男生人数,求随机变量
以上的男生人数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)根据频率分布直方图中小长方形面积等于对应区间概率及所有小长方形面积之和为1得![]() ,解得
,解得![]() .(2)根据平均数等于组中值与对应概率乘积的和得平均值,(3)先确定随机变量的取法:
.(2)根据平均数等于组中值与对应概率乘积的和得平均值,(3)先确定随机变量的取法: ![]() .再利用组合数求对应概率,列表可得分布列.最后根据数学期望公式求期望.
.再利用组合数求对应概率,列表可得分布列.最后根据数学期望公式求期望.
试题解析:解:(Ⅰ)根据题意得: ![]() .
.
解得 ![]() .
.
(Ⅱ)设样本中男生身高的平均值为![]() ,则
,则
![]()
![]()
![]() .
.
所以估计该市中学全体男生的平均身高为![]() .
.
(Ⅲ)从全市中学的男生中任意抽取一人,其身高在![]() 以上的概率约为
以上的概率约为![]() .
.
由已知得,随机变量![]() 的可能取值为
的可能取值为![]() .
.
所以![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
随机变量![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
因为![]() ~
~ ![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
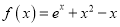 ,
, 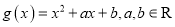 .
.(Ⅰ)当
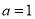 时,求函数
时,求函数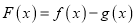 的单调区间;
的单调区间;(Ⅱ)若曲线
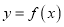 在点
在点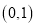 处的切线
处的切线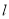 与曲线
与曲线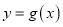 切于点
切于点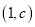 ,求
,求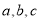 的值;
的值;(Ⅲ)若
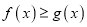 恒成立,求
恒成立,求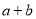 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
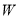 :
: 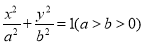 的上下顶点分别为
的上下顶点分别为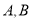 ,且点
,且点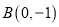 .
. 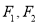 分别为椭圆
分别为椭圆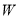 的左、右焦点,且
的左、右焦点,且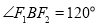 .
. (Ⅰ)求椭圆
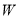 的标准方程;
的标准方程;(Ⅱ)点
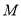 是椭圆上异于
是椭圆上异于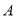 ,
, 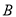 的任意一点,过点
的任意一点,过点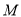 作
作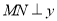 轴于
轴于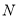 ,
, 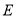 为线段
为线段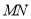
的中点.直线
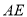 与直线
与直线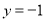 交于点
交于点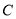 ,
, 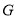 为线段
为线段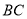 的中点,
的中点, 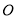 为坐标原点.求
为坐标原点.求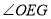 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
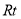 △
△ 中,
中, 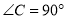 ,
, 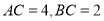 ,
, 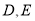 分别为边
分别为边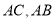 的中点,点
的中点,点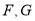 分别为线段
分别为线段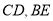 的中点.将△
的中点.将△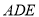 沿
沿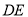 折起到△
折起到△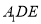 的位置,使
的位置,使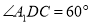 .点
.点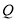 为线段
为线段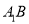 上的一点,如图2.
上的一点,如图2.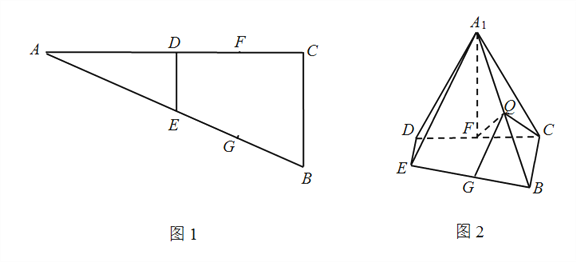
(Ⅰ)求证:
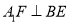 ;
;(Ⅱ)线段
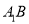 上是否存在点
上是否存在点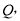 使得
使得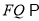 平面
平面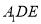 ?若存在,求出
?若存在,求出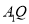 的长,若不存在,请说明理由;
的长,若不存在,请说明理由;(Ⅲ)当
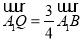 时,求直线
时,求直线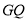 与平面
与平面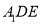 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|y=2x+1},B={y|y=x2+x+1,x∈R},则A∩B=( )
A.{(0,1)∪(1,3)}
B.R
C.(0,+∞)
D.[ ,+∞)
,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知F1、F2分别是双曲线
 ﹣
﹣  =1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,OF1为半径的圆与双曲线在第一象限的交点为P,则当△PF1F2的面积等于a2时,双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,OF1为半径的圆与双曲线在第一象限的交点为P,则当△PF1F2的面积等于a2时,双曲线的离心率为( )
A.
B.
C.
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx和反比例函数
 在同一坐标系中的图象大致是( )
在同一坐标系中的图象大致是( )
A.
B.
C.
D.
相关试题

