【题目】已知集合A={x|y=2x+1},B={y|y=x2+x+1,x∈R},则A∩B=( )
A.{(0,1)∪(1,3)}
B.R
C.(0,+∞)
D.[ ![]() ,+∞)
,+∞)
参考答案:
【答案】D
【解析】解:∵集合A={x|y=2x+1},可得x∈R,
∴A={x|x∈R},
∵B={y|y=x2+x+1,x∈R},y=x2+x+1=(x﹣ ![]() )2+
)2+ ![]() ,
,
∴B={y|y≥ ![]() },
},
∴A∩B={x|x≥ ![]() },
},
故选D;
【考点精析】关于本题考查的集合的交集运算和二次函数的性质,需要了解交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立;当
B,反之也成立;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能得出正确答案.
上递减才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
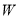 :
: 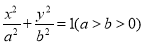 的上下顶点分别为
的上下顶点分别为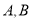 ,且点
,且点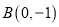 .
. 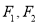 分别为椭圆
分别为椭圆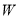 的左、右焦点,且
的左、右焦点,且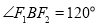 .
. (Ⅰ)求椭圆
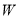 的标准方程;
的标准方程;(Ⅱ)点
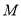 是椭圆上异于
是椭圆上异于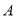 ,
, 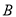 的任意一点,过点
的任意一点,过点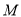 作
作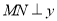 轴于
轴于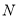 ,
, 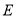 为线段
为线段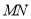
的中点.直线
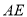 与直线
与直线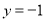 交于点
交于点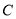 ,
, 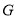 为线段
为线段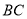 的中点,
的中点, 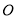 为坐标原点.求
为坐标原点.求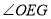 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
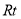 △
△ 中,
中, 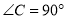 ,
, 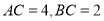 ,
, 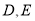 分别为边
分别为边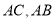 的中点,点
的中点,点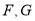 分别为线段
分别为线段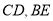 的中点.将△
的中点.将△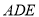 沿
沿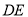 折起到△
折起到△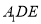 的位置,使
的位置,使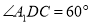 .点
.点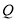 为线段
为线段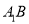 上的一点,如图2.
上的一点,如图2.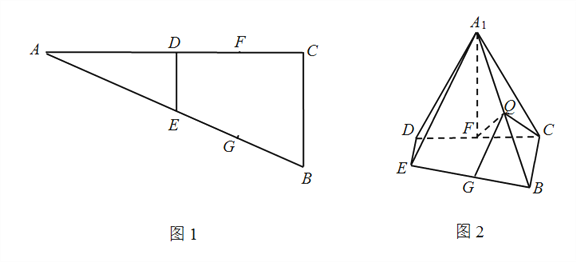
(Ⅰ)求证:
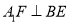 ;
;(Ⅱ)线段
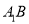 上是否存在点
上是否存在点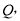 使得
使得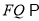 平面
平面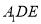 ?若存在,求出
?若存在,求出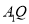 的长,若不存在,请说明理由;
的长,若不存在,请说明理由;(Ⅲ)当
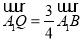 时,求直线
时,求直线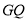 与平面
与平面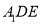 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
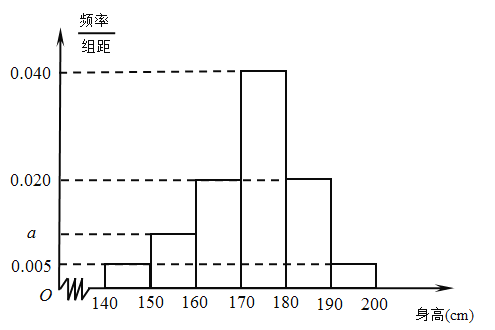
(Ⅰ)求
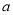 的值;
的值;(Ⅱ)假设同组中的每个数据用该组区间的中点值代替,估计该市中学生中的全体男生的平均身高;
(Ⅲ)从该市的中学生中随机抽取一名男生,根据直方图中的信息,估计其身高在180 cm 以上的概率.若从全市中学的男生(人数众多)中随机抽取
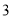 人,用
人,用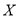 表示身高在
表示身高在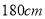 以上的男生人数,求随机变量
以上的男生人数,求随机变量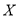 的分布列和数学期望
的分布列和数学期望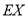 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知F1、F2分别是双曲线
 ﹣
﹣  =1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,OF1为半径的圆与双曲线在第一象限的交点为P,则当△PF1F2的面积等于a2时,双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,OF1为半径的圆与双曲线在第一象限的交点为P,则当△PF1F2的面积等于a2时,双曲线的离心率为( )
A.
B.
C.
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx和反比例函数
 在同一坐标系中的图象大致是( )
在同一坐标系中的图象大致是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准
 (吨),用水量不超过
(吨),用水量不超过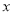 的部分按平价收费,超过
的部分按平价收费,超过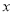 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照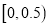 ,
,  ,…,
,…,  分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.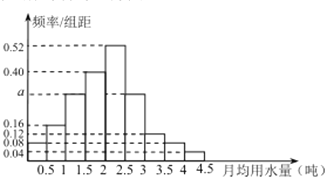
(Ⅰ)求直方图中
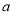 的值;
的值;(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使
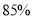 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准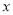 (吨),估计
(吨),估计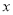 的值,并说明理由;
的值,并说明理由;
相关试题

