【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若曲线![]() 在点
在点![]() 处的切线
处的切线![]() 与曲线
与曲线![]() 切于点
切于点![]() ,求
,求![]() 的值;
的值;
(Ⅲ)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先明确函数定义域,再求函数导数![]() ,根据导函数符号确定单调区间,(2)由导数几何意义得切线斜率为
,根据导函数符号确定单调区间,(2)由导数几何意义得切线斜率为![]() ,则得
,则得![]() ,
, ![]() .即得
.即得![]() (3)不等式恒成立问题,一般转化为对应函数
(3)不等式恒成立问题,一般转化为对应函数![]() 最值问题:先利用导数研究函数最值:
最值问题:先利用导数研究函数最值: ![]() 当
当![]() 时,
时, ![]() 在
在![]() 上单调递增. 仅当
上单调递增. 仅当![]() 时满足条件,此时
时满足条件,此时![]() ;当
;当![]() 时,
时, ![]() 先减后增,
先减后增, ![]() ,再变量分离转化为
,再变量分离转化为![]() ,最后利用导数研究函数
,最后利用导数研究函数
![]() 最值,可得
最值,可得![]() 的最大值.
的最大值.
试题解析:解:(Ⅰ) ![]() ,则
,则![]() .
.
令![]() 得
得![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
令![]() 得
得![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
(Ⅱ)因为![]() ,所以
,所以![]() ,所以
,所以![]() 的方程为
的方程为![]() .
.
依题意, ![]() ,
, ![]() .
.
于是![]() 与抛物线
与抛物线![]() 切于点
切于点![]() ,
,
由![]() 得
得![]() .
.
所以![]()
(Ⅲ)设![]() ,则
,则![]() 恒成立.
恒成立.
易得![]()
(1)当![]() 时,
时,
因为![]() ,所以此时
,所以此时![]() 在
在![]() 上单调递增.
上单调递增.
①若![]() ,则当
,则当![]() 时满足条件,此时
时满足条件,此时![]() ;
;
②若![]() ,取
,取![]() 且
且![]()
此时![]() ,所以
,所以![]() 不恒成立.
不恒成立.
不满足条件;
(2)当![]() 时,
时,
令![]() ,得
,得![]() 由
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
要使得“![]() 恒成立”,必须有
恒成立”,必须有
“当![]() 时,
时, ![]() ”成立.
”成立.
所以![]() .则
.则![]()
令![]() 则
则![]()
令![]() ,得
,得![]() 由
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() 所以
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以,当![]() 时,
时, ![]()
从而,当![]() 时,
时, ![]() 的最大值为
的最大值为![]() .
.
综上, ![]() 的最大值为
的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下三个命题中:
①设有一个回归方程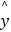 =2﹣3x,变量x增加一个单位时,y平均增加3个单位;
=2﹣3x,变量x增加一个单位时,y平均增加3个单位;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
其中真命题的个数为( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为
 (
( ,且
,且 );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )A. 每场比赛第一名得分
 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
-
科目: 来源: 题型:
查看答案和解析>>【题目】各项均为非负整数的数列
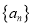 同时满足下列条件:
同时满足下列条件:①
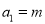
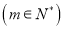 ;②
;②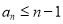
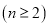 ;③
;③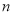 是
是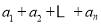 的因数(
的因数(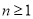 ).
).(Ⅰ)当
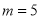 时,写出数列
时,写出数列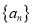 的前五项;
的前五项; (Ⅱ)若数列
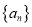 的前三项互不相等,且
的前三项互不相等,且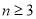 时,
时, 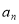 为常数,求
为常数,求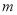 的值;
的值;(Ⅲ)求证:对任意正整数
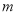 ,存在正整数
,存在正整数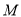 ,使得
,使得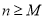 时,
时, 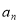 为常数.
为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
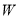 :
: 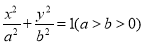 的上下顶点分别为
的上下顶点分别为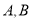 ,且点
,且点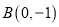 .
. 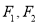 分别为椭圆
分别为椭圆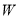 的左、右焦点,且
的左、右焦点,且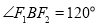 .
. (Ⅰ)求椭圆
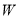 的标准方程;
的标准方程;(Ⅱ)点
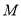 是椭圆上异于
是椭圆上异于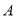 ,
, 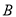 的任意一点,过点
的任意一点,过点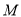 作
作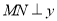 轴于
轴于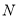 ,
, 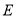 为线段
为线段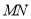
的中点.直线
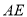 与直线
与直线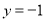 交于点
交于点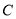 ,
, 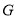 为线段
为线段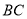 的中点,
的中点, 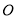 为坐标原点.求
为坐标原点.求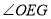 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
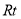 △
△ 中,
中, 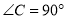 ,
, 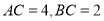 ,
, 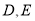 分别为边
分别为边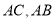 的中点,点
的中点,点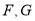 分别为线段
分别为线段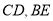 的中点.将△
的中点.将△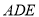 沿
沿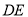 折起到△
折起到△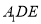 的位置,使
的位置,使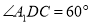 .点
.点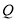 为线段
为线段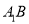 上的一点,如图2.
上的一点,如图2.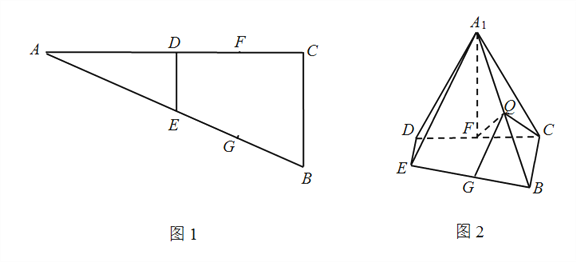
(Ⅰ)求证:
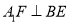 ;
;(Ⅱ)线段
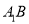 上是否存在点
上是否存在点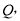 使得
使得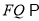 平面
平面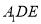 ?若存在,求出
?若存在,求出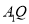 的长,若不存在,请说明理由;
的长,若不存在,请说明理由;(Ⅲ)当
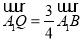 时,求直线
时,求直线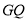 与平面
与平面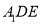 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
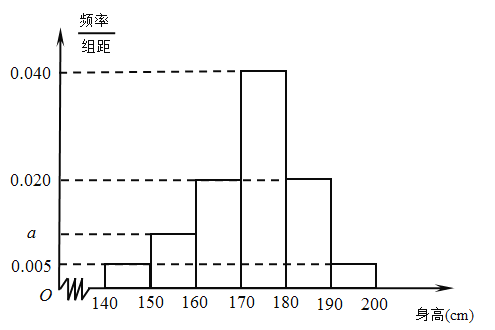
(Ⅰ)求
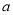 的值;
的值;(Ⅱ)假设同组中的每个数据用该组区间的中点值代替,估计该市中学生中的全体男生的平均身高;
(Ⅲ)从该市的中学生中随机抽取一名男生,根据直方图中的信息,估计其身高在180 cm 以上的概率.若从全市中学的男生(人数众多)中随机抽取
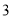 人,用
人,用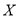 表示身高在
表示身高在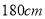 以上的男生人数,求随机变量
以上的男生人数,求随机变量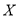 的分布列和数学期望
的分布列和数学期望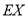 .
.
相关试题

