【题目】某地一商场记录了![]() 月份某
月份某![]() 天当中某商品的销售量
天当中某商品的销售量![]() (单位:
(单位:![]() )与该地当日最高气温
)与该地当日最高气温![]() (单位:
(单位:![]() )的相关数据,如下表:
)的相关数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)试求![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月某日的最高气温是
月某日的最高气温是![]() ,试用所求回归方程预测这天该商品的销售量;
,试用所求回归方程预测这天该商品的销售量;
(3)假定该地![]() 月份的日最高气温
月份的日最高气温![]() ,其中
,其中![]() 近似取样本平均数
近似取样本平均数![]() ,
,![]() 近似取样本方差
近似取样本方差![]() ,试求
,试求![]() .
.
附:参考公式和有关数据 ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,且
,且![]() .
.
参考答案:
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]() .
.
【解析】试题分析:(1)根据表格所给数据及平均数公式可求出![]() 与
与![]() 的值,从而可得样本中心点的坐标,再求出公式
的值,从而可得样本中心点的坐标,再求出公式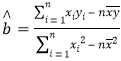 中所需数据,求出
中所需数据,求出![]() ,结合样本中心点的性质可得
,结合样本中心点的性质可得![]() ,进而可得
,进而可得![]() 关于
关于![]() 的回归方程;(2)由
的回归方程;(2)由![]() 知,
知,![]() 与
与![]() 负相关,将
负相关,将![]() 代入回归方程即可预测当日销售量;(3)由(1)知
代入回归方程即可预测当日销售量;(3)由(1)知![]() ,
,![]() ,所以
,所以![]()
![]()
![]()
![]()
![]() .
.
试题解析:(1)由题意,![]() ,
,![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]() .
.
所以所求回归直线方程为![]() .
.
(2)由![]() 知,
知,![]() 与
与![]() 负相关.将
负相关.将![]() 代入回归方程可得,
代入回归方程可得,
![]() ,
,
即可预测当日销售量为![]() .
.
(3)由(1)知![]() ,
,![]() ,所以
,所以![]()
![]()
![]()
![]()
![]() .
.
【方法点晴】本题主要考查线性回归方程及其应用、正态分布的应用,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ; 回归直线过样本点中心
; 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若
 在定义域上是增函数,求
在定义域上是增函数,求 的取值范围;
的取值范围;(2)若存在
 ,使得
,使得 ,求
,求 的值,并说明理由.
的值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 是参数).以坐标原点为极点,
是参数).以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.(1)求
 的直角坐标方程和
的直角坐标方程和 的普通方程;
的普通方程;(2)
 与
与 相交于
相交于 两点,设点
两点,设点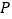 为
为 上异于
上异于 的一点,当
的一点,当 面积最大时,求点
面积最大时,求点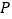 到
到 的距离.
的距离. -
科目: 来源: 题型:
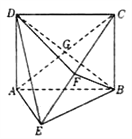
查看答案和解析>>【题目】如图所示,矩形
 中,
中,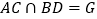 ,
,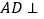 平面
平面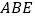 ,
,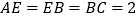 ,
,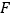 为
为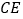 上的点,且
上的点,且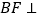 平面
平面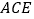 .
.
(1)求证:
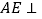 平面
平面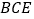 ;
;(2)求平面
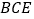 与平面
与平面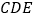 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018甘肃兰州市高三一诊】已知圆
 :
:  ,过
,过 且与圆
且与圆 相切的动圆圆心为
相切的动圆圆心为 .
.(I)求点
 的轨迹
的轨迹 的方程;
的方程;(II)设过点
 的直线
的直线 交曲线
交曲线 于
于 ,
,  两点,过点
两点,过点 的直线
的直线 交曲线
交曲线 于
于 ,
,  两点,且
两点,且 ,垂足为
,垂足为 (
( ,
,  ,
,  ,
,  为不同的四个点).
为不同的四个点).①设
 ,证明:
,证明:  ;
;②求四边形
 的面积的最小值.
的面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]
在直角坐标系
 中,以坐标原点为极点,
中,以坐标原点为极点, 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线 的参数方程是
的参数方程是 (
( 是参数),圆
是参数),圆 的极坐标方程为
的极坐标方程为 .
.(1)求圆心
 的直角坐标;
的直角坐标;(2)由直线
 上的点向圆
上的点向圆 引切线,并切线长的最小值.
引切线,并切线长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,且
,且 ,若以
,若以 为左右焦点的椭圆
为左右焦点的椭圆 经过点
经过点 .
.(1)求
 的标准方程;
的标准方程;(2)设过
 右焦点且斜率为
右焦点且斜率为 的动直线与
的动直线与 相交于
相交于 两点,探究在
两点,探究在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得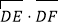 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

