【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在定义域上是增函数,求
在定义域上是增函数,求![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使得
,使得![]() ,求
,求![]() 的值,并说明理由.
的值,并说明理由.
参考答案:
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)问题等价于![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,
,![]() ,进而求最值即可.
,进而求最值即可.
(2)取![]() ,易得
,易得![]() ,所以存在整数
,所以存在整数![]() ,当
,当![]() 时,
时,![]() ,令
,令![]() ,令
,令![]() ,证明
,证明![]() 时不等式成立即可.
时不等式成立即可.
试题解析:
(1)因为![]() 在定义域上为增函数.
在定义域上为增函数.
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,
,![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上为减函数,故
上为减函数,故![]() ,所以
,所以![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.
(2)因为![]() ,
,
取![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() .
.
所以存在整数![]() ,当
,当![]() 时,
时,![]() .
.
令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() .
.
![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:

所以![]() 时,
时,![]() 取到最小值,且最小值为
取到最小值,且最小值为![]() .
.
即![]() .
.
令![]() ,则
,则![]() ,
,
令![]() ,由
,由![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.
因此![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.
综上,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,侧棱
中,侧棱 垂直于底面
垂直于底面 ,
, ,
, ,
, 为
为 的中点,
的中点, 平行于
平行于 ,
, 平行于面
平行于面 ,
, .
.
(1)求
 的长;
的长;(2)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
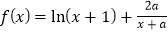 .
.(1)讨论函数
 的单调性;
的单调性;(2)若函数
 存在两个极值点
存在两个极值点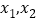 且满足
且满足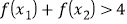 ,求
,求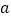 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
 (单位:千元)对年销售量
(单位:千元)对年销售量 (单位:
(单位: )和年利润
)和年利润 (单位:千元)的影响,对近13年的宣传费
(单位:千元)的影响,对近13年的宣传费 和年销售量
和年销售量
 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
由散点图知,按
 建立
建立 关于
关于 的回归方程是合理的.令
的回归方程是合理的.令 ,则
,则 ,经计算得如下数据:
,经计算得如下数据:






10.15
109.94
0.16
-2.10
0.21
21.22
(1)根据以上信息,建立
 关于
关于 的回归方程;
的回归方程;(2)已知这种产品的年利润
 与
与 的关系为
的关系为 .根据(1)的结果,求当年宣传费
.根据(1)的结果,求当年宣传费 时,年利润的预报值是多少?
时,年利润的预报值是多少?附:对于一组数据
 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 是参数).以坐标原点为极点,
是参数).以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.(1)求
 的直角坐标方程和
的直角坐标方程和 的普通方程;
的普通方程;(2)
 与
与 相交于
相交于 两点,设点
两点,设点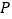 为
为 上异于
上异于 的一点,当
的一点,当 面积最大时,求点
面积最大时,求点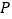 到
到 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形
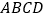 中,
中,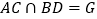 ,
,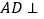 平面
平面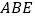 ,
,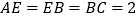 ,
,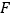 为
为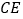 上的点,且
上的点,且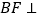 平面
平面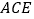 .
.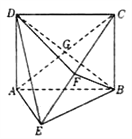
(1)求证:
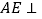 平面
平面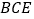 ;
;(2)求平面
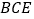 与平面
与平面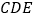 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地一商场记录了
 月份某
月份某 天当中某商品的销售量
天当中某商品的销售量 (单位:
(单位: )与该地当日最高气温
)与该地当日最高气温 (单位:
(单位: )的相关数据,如下表:
)的相关数据,如下表:











(1)试求
 与
与 的回归方程
的回归方程 ;
;(2)判断
 与
与 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地 月某日的最高气温是
月某日的最高气温是 ,试用所求回归方程预测这天该商品的销售量;
,试用所求回归方程预测这天该商品的销售量;(3)假定该地
 月份的日最高气温
月份的日最高气温 ,其中
,其中 近似取样本平均数
近似取样本平均数 ,
, 近似取样本方差
近似取样本方差 ,试求
,试求 .
.附:参考公式和有关数据
 ,
, ,
, ,若
,若 ,则
,则 ,且
,且 .
.
相关试题

