【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
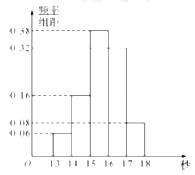
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
(Ⅰ)根据频率分布直方图,估计这50名学生百米测试成绩的中位数和平均数(精确到0.1).
(Ⅱ)若从第一、五组中随机取出三名学生成绩,设取自第一组的个数为![]() ,求
,求![]() 的分布列,期望及方差.
的分布列,期望及方差.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据频率分布直方图,计算平均值,求中位数;(2)7名学生取三人,写出随机变量的可能取值0,1,2,3,计算其相应概率,列出分布列,求期望方差.
试题解析:(Ⅰ)由频率分布直方图知,百米测试成绩的平均值为:
![]()
![]()
![]()
![]()
中位数为: ![]()
![]()
(Ⅱ)第一组人数为![]() 人,第五组人数为
人,第五组人数为![]() 人,故第一和第五组总共7名学生成绩.
人,故第一和第五组总共7名学生成绩. ![]() 的可能取值为0,1,2,3.则
的可能取值为0,1,2,3.则
![]()
![]()
![]()
![]()
所以![]() 的分布列为:
的分布列为:
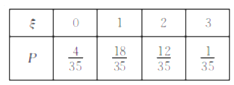
所以![]()
![]() .
.
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C经过点
 ,且圆心
,且圆心 在直线
在直线 上,又直线
上,又直线 与圆C交于P,Q两点.
与圆C交于P,Q两点.(1)求圆C的方程;
(2)若
 ,求实数
,求实数 的值;
的值;(3)过点
 作直线
作直线 ,且
,且 交圆C于M,N两点,求四边形
交圆C于M,N两点,求四边形 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
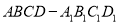 中,
中,  为棱
为棱 上一动点,
上一动点, 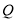 为底面
为底面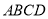 上一动点,
上一动点, 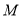 是
是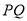 的中点,若点
的中点,若点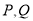 都运动时,点
都运动时,点 构成的点集是一个空间几何体,则这个几何体是
构成的点集是一个空间几何体,则这个几何体是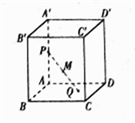
A. 棱柱 B. 棱台 C. 棱锥 D. 球的一部分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的半径为2,圆心在
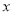 轴的正半轴上,直线
轴的正半轴上,直线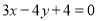 与圆C相切.
与圆C相切.(1)求圆C的方程;
(2)过点
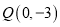 的直线
的直线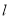 与圆C交于不同的两点
与圆C交于不同的两点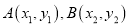 ,且当
,且当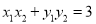 时,求
时,求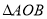 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某四棱锥的三视图如图所示,该四棱锥外接球的体积为( )
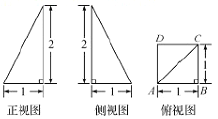
A.
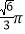 B.
B. 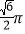 C.
C. 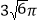 D.
D. 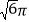
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+α)(A>0,ω>0,﹣
 <α<
<α<  )的最小正周期是π,且当x=
)的最小正周期是π,且当x=  时,f(x)取得最大值2.
时,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的图象(要列表);
(2)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】国Ⅳ标准规定:轻型汽车的屡氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆,对其氮氧化物的排放量进行检测,检测结果记录如表(单位:mg/km)
A
85
80
85
60
90
B
70
x
95
y
75
由于表格被污损,数据x,y看不清,统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等,方差也相等.
(1)求表格中x与y的值;
(2)从被检测的5辆B种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km”的车辆数为X,求X=1时的概率.
相关试题

