【题目】已知函数f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且当x=
)的最小正周期是π,且当x= ![]() 时,f(x)取得最大值2.
时,f(x)取得最大值2.
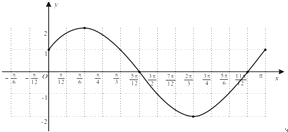
(1)求f(x)的解析式,并作出f(x)在[0,π]上的图象(要列表);
(2)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
参考答案:
【答案】
(1)解:因为函数f(x)的最小正周期是π,所以ω=2.
又因为 ![]() 时,f(x)取得最大值2.所以A=2,
时,f(x)取得最大值2.所以A=2,
同时 ![]() ,
, ![]() ,∵
,∵ ![]() ∴
∴ ![]() ,
,
∴函数y=f(x)的解析式 ![]() .
.
∵x∈[0,π],∴ ![]() ,列表如下:
,列表如下:
|
|
| π |
| 2π |
|
x | 0 |
|
|
|
| x |
f(x) | 1 | 2 | 0 | ﹣2 | 0 | 1 |
描点、连线得下图
(2)解:由已知得y=g(x)=f(x﹣m)= ![]() 是偶函数,
是偶函数,
所以 ![]() ,
, ![]() ,
,
又因为m>0,所以m的最小值为 ![]()
【解析】(1)由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,用五点法作函数y=Asin(ωx+φ)在一个周期上的图象.(2)利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的奇偶性,求得m的最小值.
【考点精析】本题主要考查了五点法作函数y=Asin(ωx+φ)的图象和函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线);图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的半径为2,圆心在
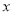 轴的正半轴上,直线
轴的正半轴上,直线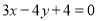 与圆C相切.
与圆C相切.(1)求圆C的方程;
(2)过点
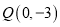 的直线
的直线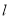 与圆C交于不同的两点
与圆C交于不同的两点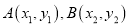 ,且当
,且当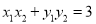 时,求
时,求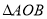 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组
 ,第二组
,第二组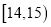 ,…,第五组
,…,第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.(Ⅰ)根据频率分布直方图,估计这50名学生百米测试成绩的中位数和平均数(精确到0.1).
(Ⅱ)若从第一、五组中随机取出三名学生成绩,设取自第一组的个数为
 ,求
,求 的分布列,期望及方差.
的分布列,期望及方差.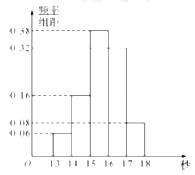
-
科目: 来源: 题型:
查看答案和解析>>【题目】某四棱锥的三视图如图所示,该四棱锥外接球的体积为( )
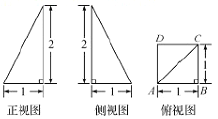
A.
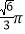 B.
B. 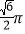 C.
C. 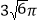 D.
D. 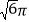
-
科目: 来源: 题型:
查看答案和解析>>【题目】国Ⅳ标准规定:轻型汽车的屡氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆,对其氮氧化物的排放量进行检测,检测结果记录如表(单位:mg/km)
A
85
80
85
60
90
B
70
x
95
y
75
由于表格被污损,数据x,y看不清,统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等,方差也相等.
(1)求表格中x与y的值;
(2)从被检测的5辆B种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km”的车辆数为X,求X=1时的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,边AB、AD的长分别为2,1,若M,N分别是边BC、CD上的点,且满足
 =
= 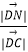 =λ.
=λ. 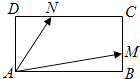
(1)当λ= 时,求向量
时,求向量 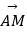 和
和 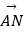 夹角的余弦值;
夹角的余弦值;
(2)求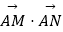 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
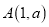 ,圆
,圆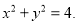
(1)过点
 的圆的切线只有一条,求
的圆的切线只有一条,求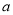 的值及切线方程;
的值及切线方程;(2)若过点
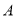 且在两坐标轴上截距相等的直线被圆截得的弦长为
且在两坐标轴上截距相等的直线被圆截得的弦长为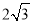 ,求
,求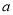 的值.
的值.
相关试题

